ABSTRACT ALGEBRA I EXAM #3

Problem 1. Let F be a field. For a polynomial 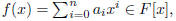we denote by

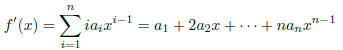
the formal derivative of f.

(a) Let

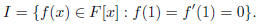
(b) Let

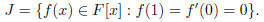
Is J an ideal of F[x]? Prove or disprove.

Solution. A subset 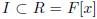is an ideal if I is a subgroup under + and is closed under multiplication
by R.

For (a), we clearly have 0 ∈ I so that if f, g∈I then (f + g)(1) = f(1) + g(1) = 0 and
(f+g)'(1) = f'(1)+g'(1) = 0 so f+g∈I, and if f∈I then (−f)(1) = −f(1) = 0 and (−f)'(1) = −f'(1) = 0
so −f∈I, hence I is a subgroup under +. Next, if f∈I and p∈R, then (pf)(1) = p(1)f(1) = 0 and

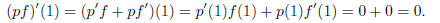
Thus I is an ideal. Indeed, I is the principal ideal generated by (x − 1)^2.

For (b), we note that J is not an ideal: we have

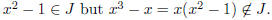
Problem 2. Determine explicitly if the matrix

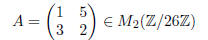
is a zerodivisor.

Solution. The matrix A is a zerodivisor. One can do this by solving linear equations over Z/26Z directly,
but here is another approach. We note that for a, b, c, d ∈R for any ring R, we have

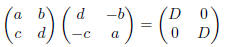
where 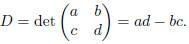We compute that det(A) = 2 − 15 =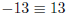 (mod 26), when

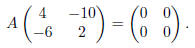
From this argument, it is easy to see that 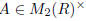if and only if 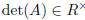, and otherwise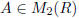
is a zerodivisor if and only if det(A) is a zerodivisor.

Problem 3. Let R be a ring.

(a) Let a∈R and suppose that 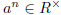for some 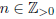. Show that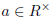
(b) Suppose that 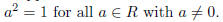Show that R is a field.

Solution. Part (a) is easy: if 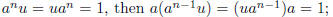by the uniqueness of left and
right inverse, we have 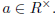(You may assume this, but for completeness: If ab = ca = 1 in a ring R, then
b = c. Indeed, since ab = 1, we have b = cab = c.)

For part (b), we note that by part (a) every 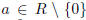is a unit, so we need only show that R is
commutative. Let a, b∈R, then by hypothesis 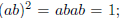then multiplying by a, b on the left and
right, respectively, we have 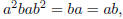so R is a field. Such fields exist, e.g. R = Z/2Z and R = Z/3Z.

Problem 4. Let R be an integral domain, and let a, b∈R. Prove that (a) = (b) if and only if a = ub for
some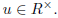

Solution. We recall that 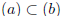if and only if b∈(a) if and only if b = ra for some r∈R. Thus (a) = (b)
if and only if b = ra and a = sb for some r, s∈R. Putting these equations together, we obtain b = (rs)b, or
b(1−rs) = 0. But since R is an integral domain, this implies that either b = 0 or rs = 1; in the former case,
we then have (b) = (0) = (a) so a = 1b = 0 in which case the result is trivially true, and in the latter case
we have a = sb where now as claimed.

Problem 5. Show that the ideal of Z[i] generated by 2 + i is maximal.

Solution. An ideal I of a commutative ring R is maximal if and only if R/I is a field. We prove that in
fact 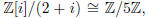which is a field since 5 is prime. We examine the set of cosets S = Z[i]/(2 + i)
and ask ourselves: what are the possible remainders? What does it mean to consider elements of Z[i]
“modulo the ideal (2 + i)”? Note that if a + bi + (2 + i)∈S, then a + bi = a + bi − b(2 + i) = a − 2b so
a+bi+(2+i) = a−2b+(2+i); but also, (2+i)(2−i) = N(2+i) = 5, so we may reduce a−2b modulo 5
as well. Therefore we define a map

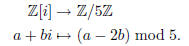
Check that this map is a ring homomorphism. It is obviously surjective, and its kernel by the above is the
ideal (2 + i). The result then follows.

Alternatively, one can “divide” an element a + bi by 2 + i, i.e. solve the equation (x + yi)(2 + i) = a + bi;
one obtains

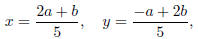
and so x, y∈Z if and only if 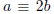(mod 5) (equivalently, 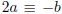(mod 5)). (This also reproves that
the kernel of the above map is the ideal 2 + i.) Now consider an ideal 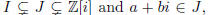then
N(a + bi) = c∈J. If gcd(c, 5) = 1, then 1∈J so J = Z[i], a contradiction. Therefore 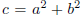must
be a multiple of 5, which can happen if and only if a 2b (mod 5) by a direct calculation, which is again a
contradiction.