Learning Outcomes for Precalculus
A. Testing Guidelines:
The following exams should be scheduled:
1. A one-hour exam at the end of the First Quarter.
2. A one session exam at the end of the Second Quarter.
3. A one-hour exam at the end of the Third Quarter.
4. A one session Final Examination.
B. Graphing calculators are required.
Learning Outcomes
For
MAT 1375/ MA 375 Precalculus
1. Students will be able to
• Find the distance and midpoint between two points.
• Determine the slope, intercept, and the equation of a line.
• Solve simple linear, quadratic and absolute value inequalities.
2. Students will be able to
• Determine the domain, and range of a given function.
• Find the sum, difference, product, quotient, and composition of functions.
• Determine the roots and relative extrema of polynomials
• Sketch the graph of polynomial, exponential and logarithmic functions with the
help of a graphing calculator
• Solve problems involving polynomial, exponential, and logarithmic functions.
• Find the amplitude, phase shift, and period of trigonometric functions.
• Students will know the domain and range of inverse trigonometric functions and
be able to calculate their values
corresponding to the special angles.
3. Students will be able to
• Write a complex number in the rectangular and polar forms.
• Multiply and divide two complex numbers.
• Use DeMoivre’s Theorem to find the nth root of a complex number.
• Find the magnitude, direction angle, horizontal, and vertical components of a
vector.
4. Students will be able identify and graph circles, parabolas, ellipses, and
hyperbolas.
5. Students will be able to find
• The nth term of arithmetic and geometric sequences.
• The nth partial sums of arithmetic and geometric sequences.
• Terms of a binomial expansion using the Binomial Theorem.
6. Students will be able to use a graphing calculator to assist in the above.
Attendance and Lateness Policy
New York City College of Technology Policy on Academic Integrity
Students and all others who work with information, ideas, texts, images, music,
inventions, and
other intellectual property owe their audience and sources accuracy and honesty
in using,
crediting, and citing sources. As a community of intellectual and professional
workers, the
College recognizes its responsibility for providing instruction in information
literacy and
academic integrity, offering models of good practice, and responding vigilantly
and
appropriately to infractions of academic integrity. Accordingly, academic
dishonesty is
prohibited in The City University of New York and at New York City College of
Technology
and is punishable by penalties, including failing grades, suspension, and
expulsion. The complete
text of the College policy on Academic Integrity may be found in the catalog.
MAT 1375 Mathematical Analysis Contemporary Precalculus: A Graphing Approach by T. Hungerford & D. J. Shaw 5th edition
| Session | Precalculus | Homework |
| 1 |
1.1 The Real Number System (pp. 2 – 13) 1.2A Special Topics: Absolute Value Equations (pp. 32 – 33) |
P. 13: 37 - 47 all, 123 - 134 all P. 33: 1 - 4 all |
| 2 |
4.6A Special Topics: Absolute Value Inequalities
(pp. 317 – 320) 2.1 Graphs (pp. 78 – 87) |
P. 320: 1 -6 all P. 89: 1 - 6 all, 9, 11, 15, 16, 19, 27 |
| 3
|
2.2 Solving Equations Graphically and Numerically
(pp. 92 – 99) 4.6 Polynomial and Rational Inequalities (pp. 308 – 315) |
P. 100: 7, 9, 21 - 27 odd P. 315: 2, 3 – 11 odd, 25-28 all Include inequalities of the form: 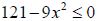 |
| 4
|
12.1
Sequences and Sums (pp. 826 ) Give the definition of a sequence on page 826 then go to section 12.2 12.2 Arithmetic Sequences (pp. 837 – 842) |
P. 842: 1, 6, 7, 17 , 25, 33, 37, 41,
45, 61, 63
|
| 5 | 12.3 Geometric Sequences (pp. 844 – 850) 12.3A Special Topics: Infinite Series (pp. 882 – 856) |
P. 850: 1 - 7 odd, 13, 15, 23, 33,
39-47 odd P. 856: 1 - 4 all, 7, 9, 10, 11, 13 |
| 6 | 1.3 The Coordinate Plane (pp. 39 – 48) | P. 48: 13 – 16 all, 27, 55 - 67 odd, 71 - 77 odd |
| 7 | First Examination | |
| 8 | 1.4 Lines (pp. 53 – 64) | P. 64: 2, 3, 5, 13-35 odd, 43-63 odd, 75,77 |
| 9 | 10.1 Circle and Ellipses (pp. 671 – 682) | P. 683: 1 - 6 all, 7 - 13 odd, 33 - 41 odd, 45, 47 |
| 10 | 10.2 Hyperbolas (pp. 686 – 697) | P. 697: 1 - 6 all, 11, 13, 15, 17, 25-31 odd |
| 11 | 10.3 Parabolas (pp. 700 – 708) | P. 710: 1 - 6 all, 17 - 25 odd, 35-39 odd, 55 - 61 odd |
| 12 |
3.1 Functions (pp. 142 – 148) 3.2 Functional Notation (pp. 151 – 158) |
P. 148: 1, 3, 11-17 odd, 23-27 all,
32, 34, 42-44 all P. 158: 1 - 5 odd, 13, 17, 21 |
| 13 |
3.2 Functional Notation 3.3A Special Topics: Graph Reading (pp. 168 – 169) |
P. 159: 27 - 31 all, 39, 41, 43 55,
57 P. 171: 12-21 all, 47, 50 |
| 14 |
3.4 Graphs and Transformations (pp. 179 – 186)
(optional) 3.5 Operations on Functions (pp. 195 – 201) |
P. 186: 1 - 8 all, 10, 12, 15, 23,
24, 26,28 P. 202: 3, 6, 11, 12-17 all, 19, 22, 25, 31-37 odd, 59 |
| 15 | Midterm Examination | |
| 16 |
4.2 Polynomial Functions (pp. 250 – 257) 4.2A Special Topics: Synthetic Division (pp. 259 – 261) |
P. 257: 11, 12, 18, 19, 23, 27,
39,41, 51, 53, 55, 56, 61 P. 262: 3, 5, 9, 10, 13, 15 |
| 17 | 4.3 Real Roots of Polynomials (pp. 262 – 268) | P. 268: 1, 3, 5, 17-19 all, 23, 25, 29, 31, 34 |
| 18 |
4.4 Graphs of Polynomial Functions (pp. 270 –
278) 4.8 Theory of Equations ( pp. 328 - 332) |
P. 278: 1 - 12 all, 19 – 24 all, 25,
29, 31, 43, 45 P. 332: 1, 3, 13, 17, 19, 21, 25, 26, 29, 30, 31, 45, 47 |
| 19 | 5.2 Exponential Functions (pp. 357 – 365) | P. 365: 1 - 5 all, 49, 51, 64, 67, 71, 72, 74 |
| 20 |
5.2A Special Topics: Compound Interest and the
Number e (pp. 369 – 373) |
P. 374: 3-9 odd, 11, 19, 23, 27, 28 |
| 21 |
5.3 Common and Natural Logarithmic Functions (pp.
375-382) 5.4 Properties of Logarithms (pp. 385 – 390) |
P. 383: 5, 9, 11, 15, 19, 23, 43, 45
57, 59, 77, 79 P. 390: 1 - 19 odd |
| 22 |
5.5 Algebraic Solutions of Exponential and
Logarithmic Equations (pp. 399– 406) |
P. 406: 1, 7 - 11 odd, 17, 19, 53 , 56 |
| 23 | Third Examination | |
| 24
|
6.4 Basic Graphs (pp. 466 – 474) (optional) 6.5 Periodic Graphs and Simple Harmonic Motion (pp. 477 – 486)
|
P. 474: 11 - 21 odd P. 486: In these problems modify the instructions to require that the graphs are plotted over one period:1, 2, 5, 6, 27, 28, 31, 32: Optional Problems: 15, 18, 23, 26 |
| 25 |
7.4 Inverse Trigonometric Functions (pp. 545 –
553) 9.1 The Complex Plane and Polar Form of Complex Numbers (pp. 626 – 630) |
P. 553: 1 - 17 odd P. 630: 1-5 odd, 9, 13, 25, 27, 37-45 odd, 53, 55, 59, 61 |
| 26 |
9.2
DeMoivre’s Theorem and nth Roots of Complex Numbers (pp. 632 – 638) |
P. 638: 1, 3, 13, 15, 19, 20, 23, 33,
41 |
| 27 | 9.3 Vectors in the Plane (pp. 639 – 650) | P. 651: 5, 11, 15, 17, 21,27-49 odd |
| 28 | 12.4 The Binomial Theorem (pp. 857 – 862) | P. 862: 3, 4, 7, 23, 24, 27, 37, 49, 51 |
| 29 | Final Examination Review | |
| 30 | Final Examination |


