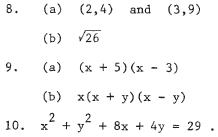REVIEW OF FUNDAMENTALS

R.R Review Exercises for Chapter

SOLUTIONS TO EVERY OTHER ODD EXERCISE

1. Subtract 2 from both sides t o get 3x = -2 . Then divide by 3 to
get x = -2/3 .

5. Expansion gives (x + 1)² - (x - 1)² = 2 = (x² + 2x + 1) - (x² - 2x + 1) =
4x . Divide both sides by 4 to get x = 1/2 .

9. 8x + 2 > 0 is equivalent is 8x > -2 . Divide both sides by 8 to get
x > -1/4 .

13. Expand to get 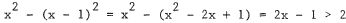. Add 1
to both sides to get 2x > 3 and divide by 2 to get x > 3/2 .

17. x² < 1 is equivalent to x² - 1 < 0 or (x + l ) ( x - 1) < 0 . One possible
solution is x < -1 and x > 1 , but this is not possible. Another
possibility is x > -1 and x < 1 . Thus, the solution is -1 < x < 1 ,
i . e . , x ∈ (-1,1) .

21.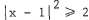 means 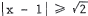, i . e . , 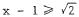or .
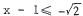For 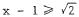, we get 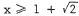. For 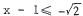, we get
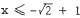. Therefore, the solution is 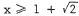or ,


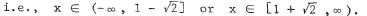
25. x³ ∈ (-8,27) implies x ∈ (-2,3) , so x < 10 and x ∈ (-2,3) means
-2 < x < 3 ; i . e . , x ∈(-2,3) .

29. 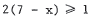is equivalent t o 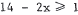or . Dividing
by -2 reverses the inequality and yields 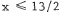. Also, 3x - 22 > 0
is equivalent t o 3x > 22 or x > 22/3 . Thus, the solution is

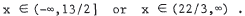
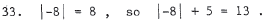
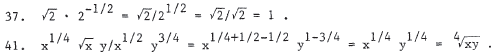
45. The distance between P₁ and P₂ is .
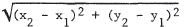In this case , it is .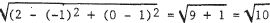

49. The point-point form of a line is .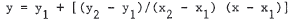
In t his case, the line is y = -1 + [ ( 3 - (-1))/(7 - 1 / 2 ) ] ( x - 1/2) =


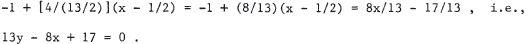
53. The point-slope form of a line is 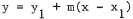. In t his case, the
line is y = 13 + (-3)(x - 3/4) = -3x + 61/4 or 4y + 3x = 61 .

57. The slope of 5y + 8x = 3 is -8/5 . Thus, the slope of a perpendicular
line is 5/8 , and the line passing through ( 1 ,1) is y = 1 + (5/8) (x - 1) ,
using point-slope form of the line . The line is y = 5x/8 + 3/8 or


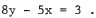
61. The equation of the circle with center (a,b) and radius r is
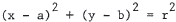. In this case, the circle is
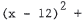
(y - 5)² = 8² or (x² - 24x + 144) + (y² - 10y + 25) = 64 or
x² - 24x + y² - 10y + 105 = 0 .

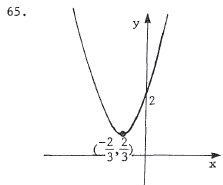Complete the square to get 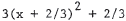. This is a parabola opening upward with vertex at (-2/3,2/3) .

69. Solve the equations simultaneously. Substitute y = x in to x² + y² = 4
to get 2x² = 4 , i . e . , x² = 2 or 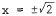. Thus, the points of inter -
section are 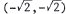and

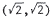
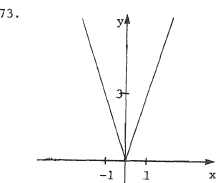	This is the graph of y = 3x if 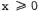; it is y = -3x if x < 0 .
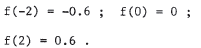	In addition t o the points in part (a), we have f(-1.5) = -0.1875 ; f(-1) = 0 ; f(-0.5) = 0.0375 ; f(0.5) = -0.0375 ;

81. If a vertical line passes through two points of the graph, it is not a
function. Thus, (a) and (c) a r e functions.

TEST FOR CHAPTER R

1. True or false :

(a) I f a > b > 0 , then 1 / a > 1 / b .
(b) The interval (2,4) contains 3 integers.
(c) If a > b > 0 , then ac > bc for constant c .
(d) The domain of is x≥ 0 .
(e) The line x = 2 has slope zero.

2.Express the solution set of x² + 3x + 2 ≥ 0 in terms of absolute
values.

3.Write equations for the following lines:

(a) The line going through (1,3) and (2,4) .
(b) The line with slope 5 and passing through (-3,2) .
(c) The line with slope -1 and y-intercept 1/2 .

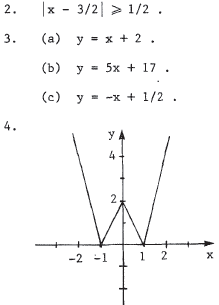
4.Sketch the graph of .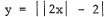

5.Do the following equations describe a circle or a parabola?



6.(a) Complete the square for the equation y² + 4y + 3 = 0 .
(b) Solve the equation in part (a) .

7.Sketch the graph of y = Ix² - 1 I .

8.(a) Find the points of intersection of the graphs of y = x² and


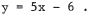
(b) Find the distance between the intersection points.

9.Factor the following expressions.



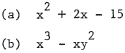
10.Dumb Donald had heard how wonderful chocolate mousse tasted, so he
decided to go on a hunting trip at Moose Valley. When he finally
spotted a moose, he chased the moose in circles around a tree located
at (-4,-2). Unfortunately for Dumb Donald, the moose ran much faster,
caught up with Dumb Donald, and trampled him. Their path was radius 7
from the tree. What is the equation of the circle?

ANSWERS TO CHAPTER TEST

1. (a) False; 1/a < 1/b .
(b) False; 2 and 4 are excluded from the interval.
(c) False; c must be positive for ac > bc .
(d) True.
(e) False; vertical lines do not have slopes.

5. (a) Circle
(b) Parabola
(c) Parabola