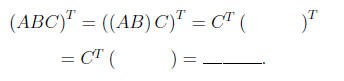Matrices and Matrix Operations

Matrix Notation:

Two ways to denote m × n matrix A:

In terms of the entries of A:

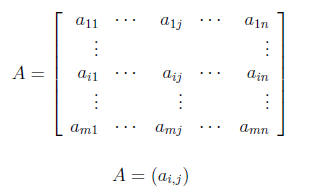
(A)_i,j is the (i, j)-entry of matrix A

In terms of the columns of A:

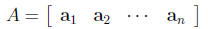
Main diagonal entries:_____

Zero matrix :

Matrix addition : Let A, B be matrices of the same size

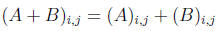
Scalar multiple :

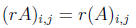
THEOREM 1

Let A, B, and C be matrices of the same size, and let r and s be scalars. Then

Matrix Multiplication

Row-Column Rule for Computing AB: Let A is m × n and B is n × p matrices
and let (AB)_ij denote the entry in the ith row and jth column of AB. Then

EXAMPLE

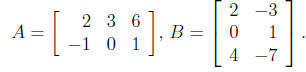
Compute AB, if it is defined.

Solution : Since A is 2 × 3 and B is 3 × 2, then AB is defined and AB is ____×____

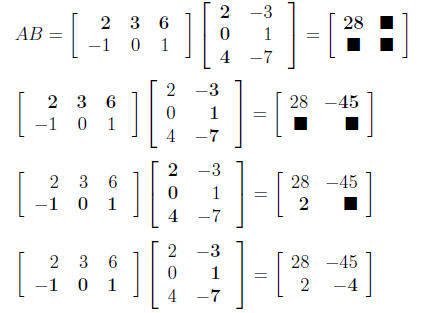
So AB =

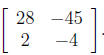
When A and B have small sizes, the Row-Column Rule is more efficient when working by
hand.

EXAMPLE: If A is 4 × 3 and B is 3 × 2, then what are the sizes of AB and BA?
Solution :

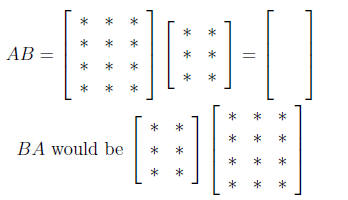
which is _______

THEOREM 2

Let A be m × n and let B and C have sizes for which the indicated sums and products
are defined.

WARNINGS

Properties above are analogous to properties of real numbers . But NOT ALL real
number properties correspond to matrix properties.
1. It is not the case that AB always equal BA.
2. Even if AB = AC, then B may not equal C.
3. It is possible for AB = 0 even if A ≠ 0 and B ≠ 0.

Powers of A

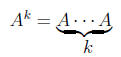
EXAMPLE:

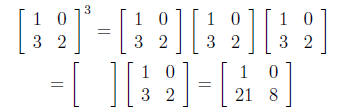
If A is m × n, the transpose of A is the n × m matrix, denoted by A^T , whose columns
are formed from the corresponding rows of A.

EXAMPLE:

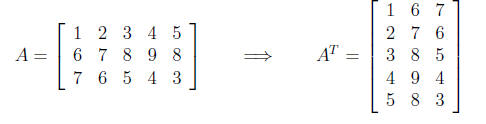
EXAMPLE:

Le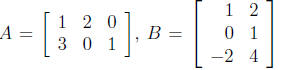t Compute AB, (AB)^T , A^TB^T and B^TA^T

Solution:

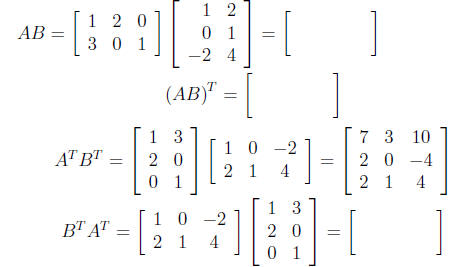
THEOREM 3

Let A and B denote matrices whose sizes are appropriate for the following sums and products .

a.(A^T)^T= A (I.e., the transpose of A^T is A)

b. (A + B)^T = A^T + B^T

c. For any scalar r, (rA)^T = rA^T

d. (AB)^T = B^TA^T (I.e. the transpose of a product of matrices equals the product of their transposes in reverse order. )

EXAMPLE: Prove that (ABC)^T = _____.

Solution: By Theorem 3d,