The ancient record of civilization in China began in the
more northern Yellow
River Valley where the Yangshao culture existed from about 5,000 to 2700 B.C.E.
These people lived in the middle and lower parts of the river valley. They
cultivated rice
and millet, kept pigs, wove baskets and made pottery without a wheel. Their
pottery was
dyed red with black geometric designs painted on it, and also pictures of fish
and human
faces. Archeologists have found pottery from these people with the symbols for
1, 2, 5,
and 7 painted on the dishes.
The next culture, one which evolved from the Yangshao, was
the Longshan
culture, which thrived from 3,000 to 2,000 B.C.E., approximately. This culture
domesticated the water buffalo, sheep and cattle. They made black pottery on a
wheel.
The pottery was not painted but decorated with grooved or raised rings.
From about 2100 to 1600 B.C.E. the Xia (or Hsia) dynasty
controlled the Yellow
River Valley. Recent discoveries have unearthed a large city with a wall and a
moat for
defensive purposes surrounding the city. This city has been dated to the early
Xia
dynasty. It is in Henan Province in today’s China.
From about 1500 to 1000 B.C.E the Shang dynasty controlled
the area with a
capital city at Anyang, also in current day Henan province, just north of the
southern
bend in the Yellow River. They also used the walled and moated city of the Xia,
mentioned above. By 1300 B.C.E. the Shang scribes had invented a brush for
writing on
bamboo strips, and had a decimal system of writing numerals. We have records of
their
kings through oracle bones, bones with inscribed writing that were used to
foretell the
future. Their writing was pictographic and had pictures of the objects referred
to in the
writing as the symbols used to write.
After the Shang dynasty we come to the period of classical
Chinese culture, that
of the Zhou (or Chou) dynasty. The early Zhou is usually dated from 1027 to 771
B.C.E. with the later Zhou extending from 770 to 256 B.C.E. During the later
Zhou
dynasty the territory controlled extended to include the more southern Yangtze
River
Valley. Also during this period the two social strata which formed the basis of
Chinese
society until 1911 were formed. These are the peasant farmer class and the
scholarly
scribes in more administrative positions. The Zhou nobility studied a curriculum
of ritual,
music, archery, horsemanship, calligraphy and mathematics. They had a
sexagesimal
calendar but a decimal arithmetic for daily life.
During the 700’s B.C.E. the first construction on the
Great Wall of China began,
and iron was introduced into China.
The period from 551 to 233 B.C.E. is known as the Hundred
Schools Period of
Chinese history. The great philosopher Lao Tsu seems to have predated Confucius
in this
period. His dates are a matter of speculation. A school of philosophy emerged
from his
teachings. He tried to reform the government. His philosophy was one of
non-striving
and non-interference, and came to be known as Taoism. He believed that his
central
principle could not be expressed in words, so his writings are contradictory and
difficult
to absorb. His ideas lead most people to a more passive role towards reform. He
taught
that the Tao is The Way, how the universe actually works, and trying to oppose
it is
fruitless activity. There were elements of mysticism in his world view.
From about 550 to 470 B.C.E. the philosopher Kung Fu Tsu
(Confucius)
expounded a moral code that included respect for the past, for elders, loyalty,
universal
education and responsible government that would bring a decent life to all of
its citizens.
He stayed away from speculations on the nature of existence and the shape of the
universe. His writings espouse a more activist way of dealing with life.
A very old book, The Book of Diverse Crafts (Kao Gong Ji
in Chinese), was
written by 476 B.C.E. with later additions in the Warring States Period. The
book
includes the state of Chinese thinking on engineering, administration,
astronomy, physics
and mathematics at that time. In the area of mathematics it contains material on
fractions,
with tenths singled out as the commonest fractions in use, the geometry of
measurement
for use in surveying and building, standard metrological units and angle
measurements of
90°, 45° and 22.5° .
The third great philosopher of China is Master Mo, who
lived about 470 to 390
B.C.E. He was a master engineer and an expert on fortifications. So he was
sought out by
rulers to help them become dominant rulers. He had a pacifist philosophy and did
not
think one should blindly follow the principles of the past, as they were
innovative in their
own day. He urged people to lead lives of self-restraint, avoiding both material
and
spiritual excesses. He evaluated actions based on their utility to promote the
good for
people. He argued for a universal benevolence and love for all people, whereas
Confucius argued for deeper love for ones’ own parents and superiors.
During the Warring States Period, from 403 to 221 B.C.E.
the Chinese used a
system of counting rods to calculate. This used bamboo, wood or ivory rods
shaped like
the numerals and arranged in columns by place value, with the larger powers of
10 going
to the left. This has a natural place value arrangement, and has no need for a
zero, as
one merely left that column empty. It carried on the earlier base 10 arithmetic.
Another old book is “The Records and Rites of the Zhou
Dynasty (Liji in
Chinese). In this book we find the curriculum for the Zhou nobility mentioned
above as
well as mention of the two main classes of administrative officials, the Sihuai
who were
statistical arithmeticians and the Chouren who were astronomers in charge of the
calendar. In the second section we find mathematical problems included to
support the
development of mathematical innovation.
The Book of Master Mo (The Mozi in Chinese) contains the
beginnings of
theoretical geometry in China. At the start are definitions of point, circle,
line, surface
and solid figures. In this book is the principle that “A stick, though half of
it be broken
off each day, will never be exhausted.” This suggests some interest in the idea
of a limit
to us, and in the infinite series
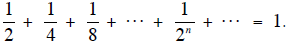
After the Zhou Dynasty the Qin (221 to 206 B.C.E.) rose to
power in China. This
Dynasty was a severe and ruthless government, which destroyed the old nobility
and
instituted large scale public works. With their military they were the first to
unify all of
China, but they did not last long. They standardized the characters used in
writing as
well as Chinese metrology. They considered scholars dangerous to their power,
and
burned all books that were not for engineering or agriculture. The Imperial
Library
was destroyed in 206 B.C.E. The famous terra cotta army, a collection of 8,099
larger
than life ceramic soldiers was buried with the first Qin emperor in an ornate
mausoleum.
This is near the Qin capitol city of Xi’an, on the Yellow river near the current
city of
Xianyang in Shaanxi province.
The Han Dynasty avoided the excesses of the Qin, and
lasted from 206 B.C.E. to
220 A.D. The Han reunited China, and extended it to cover most of central Asia.
They
reassembled old books from fragments and reopened schools. By the first century
A.D.
they were trading with Persia, Alexandrian Egypt and the Roman Empire. The
famous
Silk Road was thriving. Papermaking was invented in China by 100 A.D. It was in
Egypt by 900 A.D. and in Spain by 1150 A.D. There are two venerable texts on
Chinese
mathematics which date from this Han Dynasty. They are the Zhoubi Suanjing (The
Zhou Shadow Guage manual) and the Jiuzhang Suanshu ( The Nine Chapters on the
Mathematical Art.)
The Zhoubi Suanjing was primarily a book about astronomy
which included
plenty of mathematics. It was probably written between 100 B.C.E. and 100 A.D.
There
were two competing theories of astronomy at that time in China. Gai Tian theory
held
that the earth is an inverted basin bounded by four seas with a heaven that is a
concentric
hemisphere overhead. HunTian theory held that a rotating sphere contains the
heavenly
lights and is centered around the earth. The text records the measurements of
the moon’s
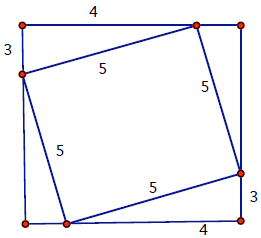
movements, those of the sun, and uses the Gougu Theorem (Pythagorean Theorem )
to
calculate distances. Here Gu refers to the length of a vertical stick in the
ground, while
Gou refers to the shadow cast by the stick. The theory of similar triangles is
part of the
mathematics used in this book. A picture like the following for 3, 4, 5
triangles appears to
justify the Gougu Theorem. It is claimed that this is just a numerical check,
but 9 + 16 =
25 is an easier check. It seems that this picture, which generalizes, can be
thought of as a
proof.
The Zhoubi Suanjing, probably written around 100 A.D. but
based on much
earlier material, gives rules for calculating with decimal fractions and
approximates
square roots, without explicitly recording how to do this. In the second half of
this
treatise, a character named Master Chen lectures on the importance of learning
to argue
both inductively from particular cases to general principles and deductively,
from
hypotheses to conclusions that follow logically from these hypotheses. It is
thus clear that
mathematics had reached a sophisticated level by the time this work was written.
The calendar in the Zhoubi Suanjing has a 365.25 day year,
with a lunar month of
29 & 499/940 days. This is 29.53085106 which compares well with our current
figure of
29.5308796 for the length of the lunar period.
The Jiuzhang Suanshu is the analog of the Elements of
Euclid for Chinese
culture. It consists of 246 problems arranged in nine chapters. It is a
practical treatise,
designed to be used to train engineers, architects and planners for their duties
in the
workplace. Here is an outline of the contents of the nine chapters:
1. Areas of squares, rectangles, triangles trapezoids,
circles and annuli .
Calculations with fractions.
2. Proportions, focusing on the exchange of millet and
rice.
3. Proportions again . This time focusing on taxation and
distribution of
properties .
4. Given a figure with a certain area or volume, to find
the dimensions of its sides.
Includes a trial and error method for finding square and cube roots .
5. Exact and approximate volumes of prisms, cylinders,
pyramids, circular cones
and tetrahedra. (assumes π = 3)
6. Fair taxes. Proportions again.
7. solving linear equations.
8. Solving simultaneous linear equations and how to
calculate with both
positive and negative numbers. (red counting rods for +, black for -)
9. Problems involving the Gougu Theorem and an
introduction to solving
quadratic equations.
The Jiuzhang Suanshu has the old Chinese algorithm for
approximating square roots to any desired degree of accuracy in chapter four.
This used to be taught in 8th grade schools in the U.S. with no explanations,
just
do the rote divisions. Here it is. Suppose you want to find the square root of
1145.
First break 1145 into two-digit pieces working from the decimal point:
 (The answer goes in the open rectangle.)
(The answer goes in the open rectangle.)
Now we start the algorithm:
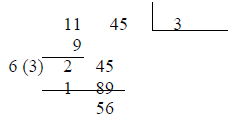
Write the nearest smaller square root of the
11 in the answer box and subtract its square
11 45 3 from 11.
Then double the 3 in the answer box, 6, and write it
out in front of the 2. Bring down the 45, and guess
the best number of the form 6x, which “divides”
our 245. It is 63. 3 x 63 = 189 subtract it from
245, and write its multiplier, 3, in the answer box, 33.
33 x 33 = 1089,
and this is the best smaller answer.
We can go on:
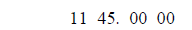
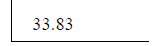
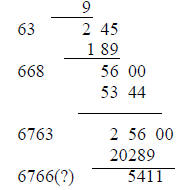
To get more accuracy, keep
on the same way, doubling the 33
and seeking a number 66x which
divides 5600.
This number is 668, 668 x 8 = 5344
which gets subtracted from 5600.
6763 x 3 = 20289
We stop. 33.83 x 33.83 = 1144.4689
Here is what is going on.
The whole area of the big square is
(10A + B)2
= 100A2 + 2(10A + B) + B2
Which one can see in the pieces of the picture.
2(10A + B) = 10·6 + 6
which is where the 2·3
comes from. |
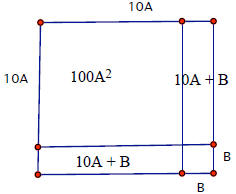 |
1089 = 332 = (10 ·3 + 3)2
so A = 3 and B = 3 |
One can draw a cubic picture of a similar sort and develop a cube root
algorithm, which
the Chinese did, and which is in chapter four of the Jiuzhang Suanshu.
Here is the place to stop and do worksheet #9, the Chinese Square Root
Algorithm.
Chapter eight has an algorithm for solving simultaneous linear equations. It is
called Gauss-Jordan elimination in the west and was discovered by Carl Friedrich
Gauss around 1800, long after the Chinese were using it. It is the basis of the
best
computer software for solving systems of linear equations. It can work for any
number of
unknowns and any number of equations. It is in most Linear Algebra courses.
Here is an example. Solve the system:
x + 2y + z = 4
3x + 8y + 7z = 20
2x + 7y + 9z = 23
One can add or subtract any multiple of any equation from any other equation
without changing what the solution is . We first use the first equation to obtain
zero in the
first terms of the last two equations:
x + 2y + z = 4
2y + 4z = 8
second Eqn -3( first Eqn )
3y + 7z = 15
Third Eqn -2( first Eqn)
x + 2y + z = 4
y + 2z = 4
½ of second Eqn.
3y + 7z = 15
x + 2y + z = 4
y + 2z = 4
third Eqn – 3(second Eqn)
z = 3
We do this to get zeros in the first two places of the third equation.
Now since z = 3, substitute in the second equation to get y = -2, and substitute
both z and y values in the first equation to get x = 5. We have the solution.



