LINEAR FUNCTIONS (2.1, 2.2, 2.3, 2.4)
• Understand the quintessential property of being linear:
equal increments in input result in equal increments in output.
• Know that the graph of a (one- variable ) linear function is a line.
• Given two different points, calculate the slope of the line through those
points.
• Given the slope of a line and a point, write an equation for the line .
• Given the slope of a line and a point, draw a graph of the line.
• Given an equation in point-slope form, slope- intercept form , or general form,
determine the slope of
the line.
• Given an equation of a line in any of the three forms, write an equivalent
equation in each of the
other two forms.
• Understand that a horizontal line has slope zero , while a vertical line has
infinite slope.
• Solve linear equations symbolically.
• Solve linear inequalities symbolically and graphically.
• Use linear functions, equations, and/or inequalities to solve applied
problems.
FUNCTION CONCEPT (1.3, 1.4, 2.5, 5.1, 5.2)
• Know that a function returns one output value for each input value.
• Be familiar with function notation and language:
Understand that in the statement "f(x) = x+5",
f is the name of the function,
x represents an input value, and
f(x) represents the output value corresponding to x.
Read f(x) as "f of x".
Given a description (formula, table, graph, or verbal) of a function and a
specific input value,
use it to evaluate a function.
• Given symbolic, numerical, graphical, or verbal descriptions for functions f
and g, give a
corresponding description for each of these:
f+g, f-g, fg, f /g, fog, gof,...
• Understand that a composition of functions is a function that applies one
function after another.
The order in which the functions are applied is explained like this :
"fog" means "do g first, then f ". Read "(fog)(x)" or "f (g(x))" as "f of
g of x".
QUADRATIC FUNCTIONS (3.1, 3.2, 3.3)
• Solve a quadratic equation by
taking square roots
factoring
completing the square
using the quadratic formula
• Know that the graph of a quadratic function is a parabola .
• Analyze a quadratic function to find its
y - intercept [by substituting 0 for x]
x - intercept(s) [by solving f(x) = 0 (because y is zero) ]
vertex [by completing the square, or use -B/(2A) for x and put into f(x) to find
y ]
long-term behavior [by looking at the sign of the x2 coefficient]
• Solve quadratic inequalities graphically (p. 207, Example1; p. 213, #1-10) and
by making a sign
chart/table (p. 210, Example 4).
• Use quadratic functions, equations, and/or inequalities to solve applied
problems, including
projectile motion and revenue problems. (p. 186, #79, 81, 83; p.204, #105)
GRAPHS AND TRANSFORMATIONS (mainly in 3.4)
• Given a point in the x-y plane, write the x- and y-coordinates. Given (x, y),
plot a point.
• Find each of the following for a given function:
| x-intercept(s) |
[ point(s) of the form (a, 0) ] |
| y-intercept |
[ point of the form (0, b) ] |
• Describe what each of the following does to the graph of f(x):
| af(x) |
[vertical scaling by a factor of a, shrinking if |a| < 1 (if a is "small")
] |
| |
[with reflection about the x-axis, if a is negative] |
| f(x)+d |
[shift up/down by d, down if d is negative] |
| f(x+b) |
[shift left/right by b, right if b is negative] |
• Given a basic graph and a formula involving one or more of these
transformations,
draw the graph of the function. [Example: given p(x), graph -¼p(-x+5) + 3.]
INVERSE FUNCTION CONCEPT (5.2)
• Understand that the inverse function f-1
is the “undo” of the original function f .
• Know that the symbol for inverse of a function f is f-1. It does not mean
reciprocal.
• Given a verbal description of a function f, give one for f-1. [opposite
operation]
• Given a formula for a function f, give a formula for f-1. ["undo" the steps]
• Given a table for a function f, give a table for f-1. [swap input and output
columns]
• Given a graph for a function f, give a graph for f-1. [swap the x and y
co-ordinates]
("flip" around the line y = x)
• Understand that logarithmic functions are inverses of exponential functions.
• Understand that the inverse of a composition of functions is the composition
of the inverse functions,
but in reverse order:
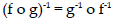
EXPONENTIAL FUNCTIONS (R.3, R.7, 5.3, 5.6)
• Know the meaning of each of the following or any combination of them :
positive exponents (R.3)
negative exponents (R.3)
exponent of zero (R.3)
fraction exponents (R.7)
• Apply the three basic properties of exponents to evaluate expressions and
solve equations.
• Recognize (without a calculator) certain powers of small whole numbers:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144,...
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000,
1, 16, 81, 256, 625, ..., 10000,
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192...
• Be able to apply your understanding to evaluate, without a calculator,
negative and/or fractional
powers of "convenient" values,
like those in your homework and supplementary exercises.
• Given a numerical or graphical description of a function, tell if the function
could be linear,
exponential, or neither. (p. 401, Example 1; p. 413, #19-24)
• Given data, find an exponential function that fits the data.
• Sketch a rough "cartoon" of an exponential function.
• Understand that an asymptote provides a long-term trend for a graph.
• Know that every exponential function can be written in the form f(x) = Cax.
• Explain, using examples, the difference between linear growth and exponential
growth.
• Describe (in words) the difference between linear and exponential growth.
• Remember that
multiplying by a positive
| 1 |
copies |
| number larger than 1 |
enlarges |
| number smaller than 1 |
reduces |
• Know that
a P% increase is the same as multiplying by (1 + 0.01P)
a P% decrease is the same as multiplying by (1 – 0.01P)
• Given an amount, apply a percent increase/decrease.
• Given an amount with a percent increase/decrease, find the original amount.
• Remember that interest rates are usually assumed to be annual.
• Know what is meant by compounding (annually, quarterly, monthly, daily).
• Given the interest rate, frequency of compounding, length of time, and present
value of an
investment, calculate the future value.
• Given the interest rate, frequency of compounding, length of time, and future
value of an investment,
calculate the present value.
LOGARITHMIC FUNCTIONS (5.4, 5.5, 5.6)
• Know that logarithms are exponents!
• Given a statement in logarithmic form, write an equivalent statement in
exponential form.
• Given a statement in exponential form, write an equivalent statement in
logarithmic form.
• Know and use the three basic properties of logarithms.
• Use properties of logarithms to solve exponential and logarithmic equations.
• Calculate logarithms of rational numbers (without a calculator).
• Given the interest rate, frequency of compounding, present value, and future
value of an investment,
calculate the length of time required.
• Given the interest rate and frequency of compounding of an investment,
calculate the doubling time,
tripling time, quadrupling time, etc.
• Solve other application problems involving exponential growth or decay,
particularly ones related to
Newton’s law of cooling (or heating) and population growth or decay.
• Sketch a rough "cartoon" of a logarithmic function.
SYSTEMS OF EQUATIONS (6.1, 6.2, 6.3, 6.4)
• Solve small (two equations) systems of linear equations algebraically.
• Solve small (two equations) systems of nonlinear equations by substitution.
• Understand that a system of linear equations may have one solution, no
solution or infinitely many
solutions.
• Understand the difference between a consistent and an inconsistent system.
• Understand the difference between an independent and a dependent system.
• Explain, in detail, the steps of Gaussian elimination with back -substitution.
• Given an application problem, write a system of linear equations for the
problem.
• Given a linear system, write the augmented matrix.
• Given an augmented matrix, write the associated linear system.
• Solve an upper-triangular system by using back-substitution.
• Recognize when a matrix corresponds to an inconsistent system.
Know that such a system has no solution.
• Recognize when a matrix corresponds to an dependent system.
Know that such a system has infinitely many solutions. Be able to find three
different solutions.
MATRIX ARITHMETIC (6.5, 6.6)
• Given a matrix, tell how many rows and how many columns it has.
• Know when matrix addition is defined.
• Know when matrix multiplication is defined.
• Understand that matrix multiplication is “row-by-column”.
• Be able to add or multiply two matrices when it is defined.
• Know what an identity matrix looks like.
• Know that the product of a matrix and its inverse is an identity matrix.
POLYNOMIAL FUNCTIONS (4.1, 4.3, 4.6)
• Divide one polynomial by another, using "synthetic division" where applicable
[only if the divisor is
of the form (x-A)].
• Solve a polynomial equation by
factoring
graphing
• Know that the graph of a polynomial function of degree n has at most (n-1)
"turns", or n "sections".
• Analyze a polynomial function to find its
| y-intercept |
[by substituting 0 for x] |
| x-intercept(s) |
[by solving f(x) = 0 (because y is zero) ] |
| long-term behavior |
[by looking at the sign of the leading coefficient ] |
• Solve polynomial inequalities graphically and by making a sign chart/table.



