Domain and Range of
Inverse Functions
•If f is one-to-one, its inverse is a
function.
•The domain of f -1 is the range of f.
•The range of f -1 is the domain of f
•Example
Problem: Verify that the inverse of
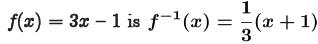
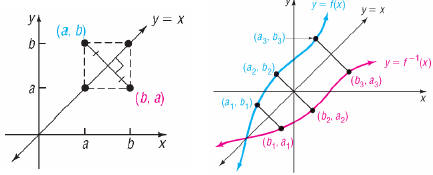
Graphs of Inverse Functions
•The graph of a function f and
its inverse f -1are symmetric with respect
to the line y = x.
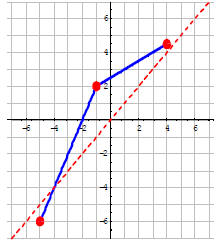
•Example.
Problem: Find the graph of the inverse
function
Answer:
Finding Inverse Functions
•If y= f(x),
•Inverse if given implicitly by x= f(y).
• Solve for y if possible to get y= f -1(x)
•Process
• Step 1: Interchange x and y to obtain an
equation x = f(y)
•Step 2: If possible, solve for yin terms of
x .
•Step 3: Check the result.
•Example.
Problem: Find the inverse of the function
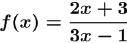
Answer :
Restricting the Domain
•If a function is not one-to-one, we can
often restrict its domain so that the
new function is one-to-one.
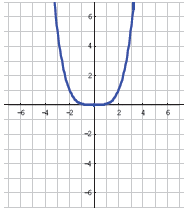
•Example.
Problem: Find the inverse of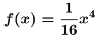 
if the domain of f is x≥0.
Answer:
Key Points
•One-to-One Functions
•Horizontal-line Test
•Inverse Functions
•Domain and Range of Inverse Functions
•Graphs of Inverse Functions
•Finding Inverse Functions
•Restricting the Domain
Exponential
Functions
Section 4.3
Exponents
•For negative exponents :
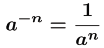
•For fractional exponents :
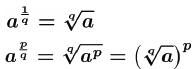
•Example.
Problem: Approximate 3πto five decimal
places.
Answer:
Laws of Exponents
•Theorem. [Laws of Exponents]
If s, t, a and bare real numbers with a >0
and b>0, then
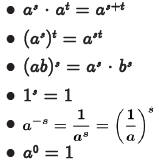
Exponential Functions
•Exponential function: function of the
form
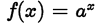
•where a is a positive real number (a>0)
•a≠1.
•Domain of f: Set of all real numbers .
Warning! This is not the same as a power
function.
(A function of the form f(x) = xn)
•Theorem.
For an exponential function
f(x) = ax, a >0, a≠1, if x is any
real number, then
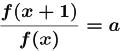
Graphing Exponential
Functions
•Example.
Problem: Graph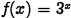 
Answer:
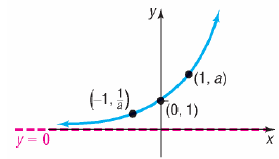
Properties of the
Exponential Function
•Properties of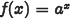 
, a >1
•Domain: All real numbers
•Range: Positive real numbers; (0, ∞)
•Intercepts:
•No x-intercepts
•y- intercept of y = 1
•x-axis is horizontal asymptote as x →-∞
•Increasing and one-to-one.
•Smooth and continuous
•Contains points (0,1), (1, a) and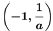 
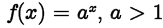
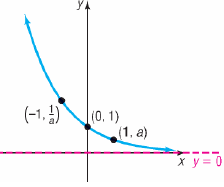
•Properties of ,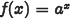
0 <a <1
•Domain: All real numbers
•Range: Positive real numbers; (0, ∞)
•Intercepts:
•No x-intercepts
•y-intercept of y= 1
•x-axis is horizontal asymptote as x →∞
•Decreasing and one-to-one.
•Smooth and continuous
•Contains points (0,1), (1, a) and
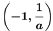
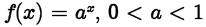
The Number e
•Number e: the number that the
expression
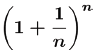
approaches as n→∞.
•Use ex or exp (x) on your calculator.
•Estimating value of e
•n= 1: 2
•n= 2: 2.25
•n= 5: 2.488 32
•n= 10: 2.593 742 460 1
•n= 100: 2.704 813 829 42
•n= 1000: 2.716 923 932 24
•n= 1,000,000,000: 2.718 281 827 10
•n= 1,000,000,000,000: 2.718 281 828 46
Exponential Equations
•If 
, then u= v
•Another way of saying that the
function
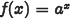is one-to-one.
•Examples.
(a) Problem: Solve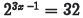 
Answer:
(b) Problem: Solve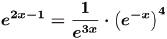 
Answer:
Key Points
•Exponents
•Laws of Exponents
•Exponential Functions
•Graphing Exponential Functions
•Properties of the Exponential Function
•The Number e
•Exponential Equations
Logarithmic
Functions
Section 4.4
Logarithmic Functions
•Logarithmic function to the base a
•a>0 and a≠1
•Denoted by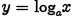 
•Read “logarithm to the base a of x ”or
“base a logarithm of x”
•Defined: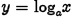 
if and only if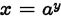 
•Inverse function of 
•Domain: All positive numbers (0,∞)
•Examples. Evaluate the following
logarithms
(a) Problem: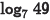
Answer:
(b) Problem: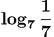
Answer:
(c) Problem: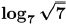
Answer:
• Examples. Change each exponential
expression to an equivalent expression
involving a logarithm
(a) Problem: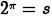
Answer:
(b) Problem: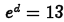 
Answer:
(c) Problem: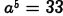 
Answer:
• Examples. Change each logarithmic
expression to an equivalent expression
involving an exponent.
(a) Problem: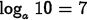
Answer:
(b) Problem: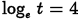 
Answer:
(c) Problem: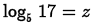 
Answer:
Domain and Range of
Logarithmic Functions
•Logarithmic function is inverse of the
exponential function.
•Domain of the logarithmic function
•Same as range of the exponential
function
•All positive real numbers, (0, ∞)
•Range of the logarithmic function
•Same as domain of the exponential
function
•All real numbers, (-∞, ∞)
•Examples. Find the domain of each function
(a) Problem:
Answer:
(b) Problem: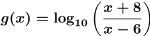 
Answer:
Graphing Logarithmic
Functions
•Example. Graph the function
Problem: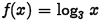 
Answer:
