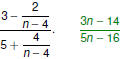FACTORING POLYNOMIALS

Outline
1 Factoring Polynomials
• Terminology
• Factoring

2 Rational Expressions
• Definition
• Manipulating Rational Expressions

Terms

Definition
The terms of an algebraic expression are those elements that are
separated by addition (that is, by plus or minus signs).

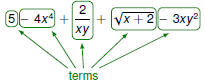
The sign of the term is important!

Monomials

Definition
Terms that contain variables with only nonnegative integer
exponents are called monomials.

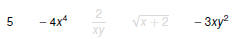
Polynomials

Definition
A polynomial is a monomial or a finite sum of monomials.

Examples of polynomials

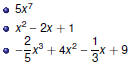
Factoring Out Monomials

The simplest form of factoring polynomials is factoring out the
highest common monomial factor .

• In x² + 3x, each term contains a factor of x.
x² + 3x = x(x + 3)

• In 3x⁴ + 12x², each term contains a factor of 3x².
3x⁴ + 12x² = 3x²(x² + 4)

• In 12a²b − 30ab + 18ab², each term contains a factor of 6ab.
12a²b − 30ab + 18ab² = 6ab(2a − 5 + 3b)

Factoring By Grouping
Sometimes we can factor out a binomial by grouping terms in
pairs, and factoring a monomial out of each pair.

• x³ + 2x² + 3x + 6
= (x³ + 2x²) + (3x + 6)
= x²(x + 2) + 3(x + 2)
= (x² + 3)(x + 2)

• 3ac + 16b − 4a − 12bc
= 3ac − 12bc − 4a + 16b
= (3ac − 12bc) + (−4a + 16b)
= 3c(a − 4b) − 4(a − 4b)
= (3c − 4)(a − 4b)

Factoring ax² + bx + c

Factoring Quadratics
To factor a quadratic of the form ax² + bx + c:

Find a pair of numbers , say r and s, whose sum is b
(r + s = b), and whose product is ac (rs = ac).

Write the quadratic as ax² + rx + sx + c.

Factor by grouping.

Example: 4x² + 11x + 6 a = 4, b = 11, c = 6

Find two numbers whose product is 24 and whose sum is 11.
r = 3, s = 8

Write the quadratic as 4x² + 3x + 8x + 6.

Factor by grouping.
4x² + 3x + 8x + 6
= (4x² + 8x) + (3x + 6)
= 4x(x + 2) + 3(x + 2)
= (4x + 3)(x + 2)

Special Factoring Patterns

• x² − y² = (x + y)(x − y)
• x³ + y³ = (x + y)(x² − xy + y²)
• x³ − y³ = (x − y)(x² + xy + y²)

Examples

Factor 9x² − 25 completely. (3x + 5)(3x − 5)

Factor 9x²y² − 64 completely. (3xy + 8)(3xy − 8)

Factor a² + 5a − 24 completely. (a + 8)(a − 3)

Factor 2x² − 7x − 30 completely. (2x + 5)(x − 6)

Factor x³ + 64 completely. (x + 4)(x² − 4x + 16)

Factor 2n² − n − 5 completely. Not factorable

Definition

Definition
The quotient of two polynomials is called a rational expression.
Examples

We will assume that all denominators represent nonzero real
numbers (so we needn’t always write things like “x ≠−2” or
“x ≠1/3”).

Simplifying

• Factor anything you can.
• Cancel factors if possible.
• Remember that rational expressions are just fractions.

We really need to work examples.

Examples

Examples
Simplify

Simplify

Simplify

Simplify
5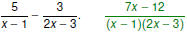

Simplify