Problem 1.
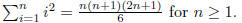
Solution . The proof will be by induction on n. The base
case is n = 1. The
left-hand side of the equation becomes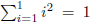 
and
the right-hand side is
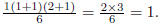Thus the base case holds.
Now assume that the above equation hold for n = k - 1
where k ∈N is some
constant such that k - 1≥1. Thus in,
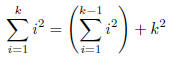
we can replace the second summaion and get ,
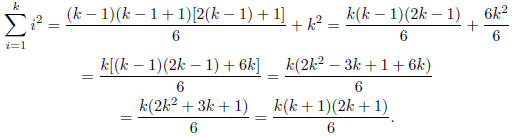
Thus the equation holds for some k given that it holds
k-1. By induction it follows
that the equation holds for all n ∈N.
Problem 2.
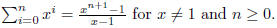
Solution . The proof is by induction on n. The base case is
n = 0. We prove it thus,
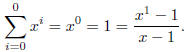
Now, assume that the equation is true for some k ∈N and n
= k - 1≥0.
Consider,
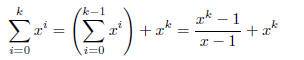
Where the second equality comes from applying the
induction hypothesis. Continuing,
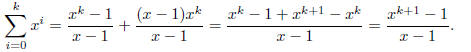
Which is the desired result for n = k. By induction, the
equation is true for all
n∈N.
Problem 3. Consider the following statement. the
sum of cubes of the first n
positive integers is equal to the square of the sum of these integers. Restate
this as
a formal mathematical theorem using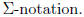 
Prove
your theorem.
Solution. Theorem 1. For n∈N and n≥1,
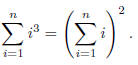
Proof. The proof is by induction on n. The base case is
when n = 1,
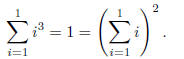
Now assume that the theorem holds for n = k - 1 for some
k∈N, k - 1≥1.
Thus we get that,
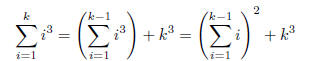
Where the last equation comes from applying the induction
hypothesis. Now we
use the fact that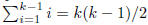
to show that,
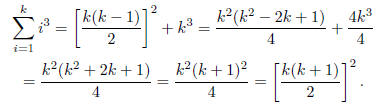
Which is the equation with n = k. Therefore, by induction,
the theorem holds.
Problem 4. n^5 - n is divisible by 5 for every
positive integer n.
Solution. The proof will follow by induction on the n. We
prove the base case,
n = 1, follows because n^5 - n = 1^5 - 1 = 0 is divisible by 5.
Now we assume that k^5-k is divisible by 5 for some
positive integer k. Consider,
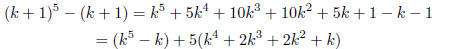
The first term is divisible by 5 because of the induction
hypothesis and the second
term is divisible by 5 because is contains a factor of 5. Thus the sum is
divisible
by 5. This proves the induction hypothesis and completes the proof.
Problem 5. Find (and prove) an exact closed form
solution to f(n) mapping the
natural numbers to the reals defined by
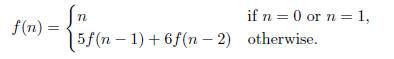
Solution. Claim.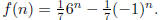 
The proof is by induction on n.
Base. (note that there are two base cases since the recurrence uses two
previous
values f (n - 1) and f(n - 2)).
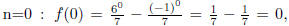and we have f(0) = 0 by
the recursive
definition of f.
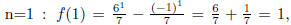and we have f(1) = 1 by
the recursive
definition of f.
Inductive Step . Assume n > 1. Assume
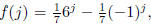for all j such
that 0 ≤ j < n. Let IH(j) be the statement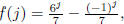 
so
we are assuming
IH(j) for 0 ≤ j < n. We need to show that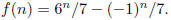 
Since n > 1, we can use the recursive definition of f to
get that
f(n) = 5f(n - 1) + 6f(n - 2).
We can use IH(n-1) and IH(n-2) to rewrite f(n-1) and
f(n-2). So from the
inductive hypothesis we get.
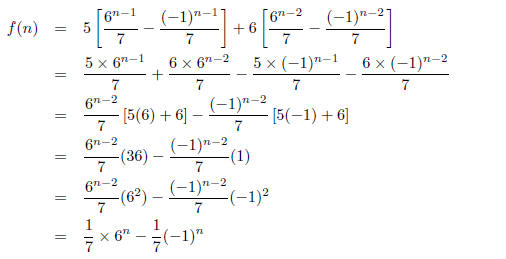
which is what we needed to show.
Problem 6. Define the following recurrence
Show that 
Solution. Proof by induction on n. Note that there
will need to be two base cases
for this induction proof. One (n = 0) is not sufficient because then our
inductive
step would have to cover 1, . . . , n. This presents a problem because our
recurrence
is not defined for n = 1. In general when there are two recursive references to
a
function like F , namely F(n - 1 and F(n - 2), two base cases are required for a
proof by induction.
Base Step. n = 0. By definition
again we have
Inductive Step. Let n≥2. Assume
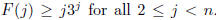This is
the inductive hypothesis. Our goal is to show that this assumption implies that
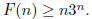Consider the recursive definition of F.
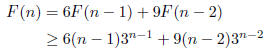
by the inductive hypothesis. Note the inequality , and that
here we have applied the
inductive hypothesis twice-once for F(n - 1) and once for F(n - 2). Continuing
on...
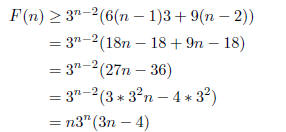
Recall that we are deaing with n≥2. In this case we have
that 3n - 4≥n. Of
course, this can also be proved by induction.
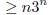
as desired. By the principle of mathematical induction we
are done.
