Linear Algebra , Section 1.9

First, some vocabulary: A function is a rule that associates objects in a set
(the domain) to a unique object in a set (the codomain).
The range or image of f is:

{y|y = f(x)}

We don’t talk about the codomain in calculus anymore for some reason... Think
of the range (or image) as a subset of the codomain.
In calculus, we have the following definitions. These are necessary before we
can talk about the inverse of a function.

• A function y = f(x) is said to be onto (its codomain) if, for every y (in
the codomain), there is an x such that y = f(x).
Note: Every function is automatically onto its image by definition (Since
we only talk about the range in calculus, this is probably why the codomain
is never mentioned anymore). Normally, the question is whether the function
is onto its codomain. For example, y = x² is not onto the real line,
but is onto its range, which is the interval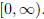
If we don’t want to specify that a function is onto its codomain, we will
say that f maps x into the codomain.

• A function y = f(x) is said to be 1 − 1 if

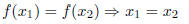
or (this is logically equivalent to the equation above):

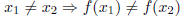
In words, this means that each element of the range came from a unique
element of the domain. In calculus, you might remember this graphically
as the horizontal line test - If any horizontal line passes through the graph
of f in more than one place, then f(x₁) = f(x₂), but x₁ is not x₂. For
example, y = x² is not 1 − 1 because (−2)² = 2², but −2 ≠ 2.

In Section 1.9, the big theorem was that:
If T : IRⁿ -> IR^m is a linear transformation, then there exists an m × n
matrix A so that

T(x) = Ax

Additionally ,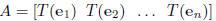

Another way to think of this is to say that every linear transformation from
IRⁿ to IR^m can be realized as matrix-vector multiplication. Now we are looking
at the equation

Ax = b

as a linear transformation, where x ∈IRⁿ is the domain, and IR^m is the
codomain.

As it turns out, linear transformations are also continuous and differentiable ,
but to show this we will need to be able to measure distances in IRⁿ and IR^m.

1 Onto

When will T(x) = Ax be onto? This would imply that for every b ∈IR^m, there
is (at least one) solution to Ax = b. This is the setup for Theorem 4, page 43.
We now list that theorem, together with our new terminology :
Theorem 4, Revised: Let A be an m× n matrix. The following are logically
equivalent:

1. The function Ax = b is onto IR^m.
2. For each b ∈IR^m, the equation Ax = b has a solution.
3. Each b in IR^m is a linear combination of the columns of A.
4. The columns of A span IR^m.
5. A has a pivot position in every row.

2 One to One

When will T(x) = Ax be 1-1? This means that the matrix equation Ax = b
always has at most one solution (it might have no solution). Let’s write out
the counterpart to Theorem 4. To neatly summarize, you should write out a
comparison chart !

The “One to One” Theorem: Let A be an m×n matrix. The following are
logically equivalent :

1. The function Ax = b is 1 − 1.
2. The equation Ax = b has at most one solution for every b
3. The equation Ax = 0 has only the trivial solution.
4. The columns of A are linearly independent.
5. A has a pivot position in every column.

3 Worked Examples

1. Let T : IR² -> IR² by mapping the span of (3, 2) and (−1, 1) to the span
of (1, 1). Find a matrix that realizes this mapping , then determine if the
mapping is 1-1 and/or onto:
The mapping is not unique in this case because the question does not
specify how the mapping performs this operation . However, since Ax is a
linear combination of the columns of A, we know that the columns of A
must be scalar multiples of (1, 1). Furthermore, we know that the span of
(3, 2) and (−1, 1), being linearly independent, is all of IR². We have lots
of choices for A; one A might be:

This mapping is neither 1-1 nor onto, since there is only one pivot and
two rows/columns.

2. Let A be m × n with m < n so that A is a “wide” matrix. If it has m
pivots, then the corresponding transformation x -> Ax will be onto IR^m,
but will not be 1 − 1 (because of the free variables ).

3. Let A be m × n with m > n so that A is a “tall” matrix. If it has the
maximum number of pivots possible, n, then the transformation x -> Ax
will be 1-1 (a pivot in every column, no free variables, so that Ax = 0 has
only the trivial solution), but A will not be onto since there is not a pivot
in every row.

NOTE: The implication of numbers 2 and 3 is that, for x -> Ax to be
1-1 and onto, the matrix must be square , and the RREF of A must be the
identity matrix.

4. Construct a mapping x -> Ax so that (−1, 1) is mapped to (3, 1) and (1, 1)
is mapped to (2, 1). State whether the mapping is 1 − 1 and/or onto:
We’ll have four unknowns for the entries of A. We cannot use our “big
theorem” since we don’t know how the mapping transforms e₁ and e₂, so
we set up some equations:

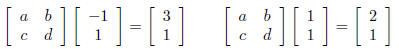
Which translates to:

Which translates to the following two augmented matrices:

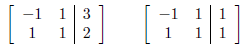
Whose RREF are:

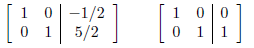
So the matrix A is 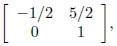and the mapping x -> Ax will be both
1 − 1 and onto.

Note: A linear mapping from IR² to IR² is uniquely defined by its action
on two points.

4 Extra Practice with Functions

We’ve introduced linear functions from IRⁿ to IR^m- how do we write nonlinear
functions F from IRⁿ to IR^m?

First note that there are n inputs and m outputs to F. We will write an
input as (x₁, . . . , x_n), and the outputs as (F₁, . . . , F_m), where each F_i maps IRⁿ
to IR. Here’s an example before we make the general statement. Here, F maps
IR² to IR²:

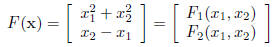
We write a generic function from IRⁿ into IR^m by its coordinate functions,

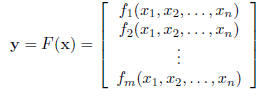
where each f_i : IRⁿ -> IR.
Here are some examples:

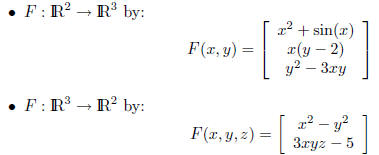
• Solving y = F(x) cannot generally be done in closed form. Normally, we
would need to approximate a solution, then find a method to give us better
and better approximations. Sometimes we get lucky, and the problem is
easy enough to solve directly- For example, solve for x, y so that:

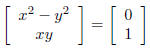
so that x² = y² and xy = 1. Therefore, (1, 1) and (−1,−1) are solutions.

Why study linear functions? While general nonlinear functions may be the
norm, many times we can replace the difficult, nonlinear function by its local,
linear approximation (remember doing that with the tangent line?)... More on
that later in class.