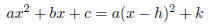1 Squares
Recall that an integer a is said to be square if for some integer we have a =
α2 - that is, a's square root is
an integer. A quadratic is said to be square if a similar condition holds -
specifically, if it is equal to the square of
some linear function (ax + b).
For any x, y we have (x + y)^2 = x^2 + 2xy + y^2 - for
example, (x + 0)^2 = x^2 (as we would expect to see),
(x+1)^2 = x^2 +2x+1, (x+2)^2 = x^2 +4x+4, and (x+3)^2 = x^2 +6x+9. These are
very convenient for a number
of reasons, but unfortunately most quadratics are not of this form, on the
bright side, we do have ways of making
them cooperate, as will be discussed after a brief side note.
2 The Symmetry of Quadratics
We can, and should, examine the symmetry of a quadratic:
recalling the quadratic formula , which states that
a polynomial f(x) = ax^2 + bx + c has roots given by
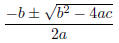
(Recall that a root of a function f is a number x such
that f(x) = 0.)
The symmetry of a quadratic is simple and important - given two points at the
same 'height' on the quadratic,
the axis of symmetry is the vertical line directly between the two points . The
roots of a quadratic are at the same
'height' (as that 'height' is, by definition, 0), so we can use these to find
the axis of symmetry.
Suppose we have some polynomial f(x) = ax^2 + bx + c, with
a ≠ 0, a line (in this case a vertical line) called
the axis of symmetry should lie directly between its two roots. (When we say
'directly between', we mean 'between
the two points in such a way that the distance from the axis to one point is the
same as the distance to the other
point', I hope that nobody who reads this will think less of me for abbreviating
in this way.) We can express the
roots of the polynomial as
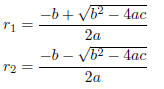
and find exactly where 'directly between' should be.
The number 'directly between' two numbers a and b is their average -(a+b)/2 . We
would then expect to see that
the axis of symmetry (whose position we will call s) would be directly between
the two roots:
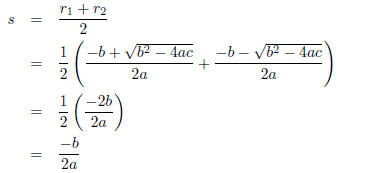
We now know where the axis of symmetry must lie: it will
be the set of points (-b/2a , y), for real numbers y - the
vertical line at x = -b/2a .
It would be helpful to know what the value of the function
f is when it touches the axis of symmetry - this will
be the value of f at the axis of symmetry, in fact. We call the point
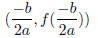
the vertex of f .
3 Completing The Square
As mentioned earlier, we have ways of letting ourselves
treat a quadratic as a square - specifically, a square of
the same shape that has been 'shifted' around a bit.
Consider the graph of y = x^2, it is a quadratic with its
vertex at (0, 0). As we will soon see, other quadratics
y = ax^2 + bx + c are not too far removed from this one .
The technique called completing the square involves
finding another way of expressing a quadratic - we want
to express our quadratic in terms of a square plus or minus a constant. As an
equation, we are trying to find an
equation of the form
and solve for d and e .
Finding d in this equation comes first. We want the only difference between ax^2
+ bx + c and a(x + d)^2 to be
a constant - specifically, e - so what we must do is find a square that has the
same coefficients for x ^2 and x as our
original polynomial.
The next steps may be more clear if we start by factoring
out a (it should be noted that we can do so because
if a = 0 our 'quadratic' is clearly an impostor), and when we factor out a we
have
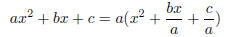
What square, then, has the same numbers in front of x^2
and x? Recall that (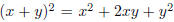
-if we
then try (x + b/2a ), we have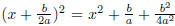 
. Don't worry
about the last term, what's important is that
the coefficients of x^2 and x are just right. Also note that
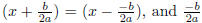is also the location of the
axis of symmetry found just a few paragraphs ago.
After finding d = b/2a , finding e is simple - referring
to the equation (1) above, all we must do is multiply out
(x + d)^2 and then cancel out like terms .
This brings us to another approach that relies on the
inherent symmetry of the quadrilateral. Suppose we have
the vertex of our quadratic (to find this, just find the axis of symmetry -
(-b/2a) - and plug that value in for x in the
quadratic - the axis of symmetry gives the x- coordinate and the value of the
function there gives the y-coordinate),
which we will refer to as (h, k) for convenience. We can then complete the
square very easily - for hopefully obvious
reasons this expression of the quadrilateral is often called the vertex form:
