1 Terminology
A matrix is a rectangular array of numbers, for example
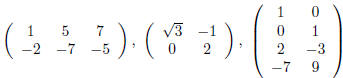 ,or
,or
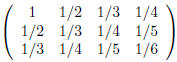
The numbers in any matrix are called its entries. The
entries of a matrix are organized into rows and
columns, which are simply the horizontal and vertical (resp.) lists of entries
appearing in the matrix. For
example, if

then the rows of M are 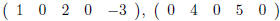 and
and 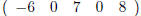 whereas the
whereas the
columns of M are
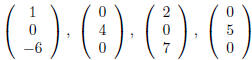 ,and
,and
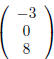 .
.
It is worth noting that an m · n matrix will have m rows
with n entries each, and n columns with m entries
each. That is, the number of entries in any row of a matrix is the number of
columns of that matrix, and
vice versa. This is readily apparent in each of the examples above.
The dimensions of a matrix are the numbers of rows and columns it has. If a
matrix has m rows and n
columns we say that it is an m · n matrix (note that we always list the number
of rows first). So, the first
four matrices above have dimensions 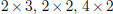 and
and 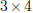 , respectively. The dimensions of the
matrix
, respectively. The dimensions of the
matrix
M are 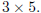 An m · n matrix is called square if m
= n. Thus, the only example of a square matrix above
An m · n matrix is called square if m
= n. Thus, the only example of a square matrix above
is the second.
So that we can more easily refer to various entries in matrices, we index the
columns of a matrix from
left to right and the rows from top to bottom. For example, the first column of
M (above) is
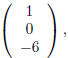
the second column is
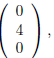
the third column is
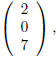
etc. The first row of M is
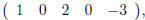 the second row is
the second row is
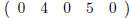 and the third row is
and the third row is
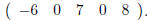 We can use this numbering scheme to easily
refer to entries in a matrix: we call the
We can use this numbering scheme to easily
refer to entries in a matrix: we call the
entry located in row i and column j the i, j-entry. For the matrix
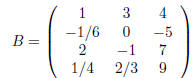
the 1, 1-entry is 1, the 3, 2-entry is -1, the 4, 3-entry
is 9 and the 2, 1-entry is -1/6.
To write down a matrix with variable entries we use variables with subscripts
that indicate their position
in the matrix, using the convention described above. A generic m· n matrix can
therefore be denoted
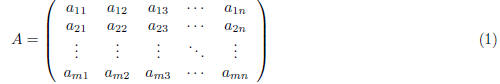
or just 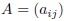 for
short.
for
short.
An m ·1 matrix has the form
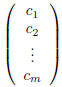
and is called, appropriately, a column vector. Notice that
since a column vector has only a single column we
have used only single subscripts to index its entries. Likewise, a 1· n matrix
looks like
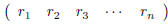
and is called a row vector. When we use the word vector
with no qualification we will usually mean a column
vector. Column vectors give us another shorthand for writing down generic
matrices. Notice that if we use
the matrix A in (1) and set
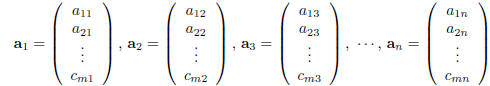
(i.e. we use the entries in the j-th column of A as the
entries in aj) then we can write
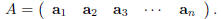
In a similar way one can also use the rows of A to express
A in terms of row vectors, but since we won't be
using this idea later we won't bother to write it out.
2 Scalar multiplication and addition of matrices
Having dispensed with the basic terminology and notation of matrices, we now
turn to how they are ma-
nipulated algebraically . We will see that it is possible to add, subtract and
multiply matrices together, but
only if certain restrictions on their dimensions are met. We begin with the
notion of scalar multiplication.
Given an m · n matrix A = (aij) and a number (scalar) c we define
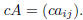
That is, cA is the matrix obtained by multiplying every
entry of A by c. As examples, if
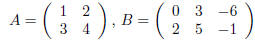
then
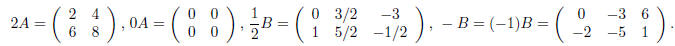
Adding two matrices is also done entry-by-entry. If A =
(aij) and B = (bij) are two m· n matrices, then
their sum is A + B = (aij +bij ). That is, the i, j-entry of A+ B is the sum of the i, j-entries of A and B. It
is important to note that is is only possible to add two matrices if they have
exactly the same dimensions.
Here's an example: if
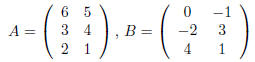
then
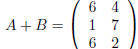
and
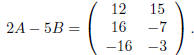
The following theorem summarizes the main · properties of
matrix addition. The proofs of these properties
follow directly from the definitions made so far and are left to the reader. We
will find it useful to be able
to refer to the m· n zero matrix , which is the matrix all of whose entries are
zero.
Theorem ·1. Let A, B and C be m· n matrices, let c be a real number and let
0 denote the m· n zero
matrix. Then
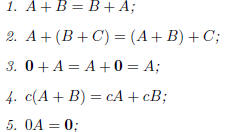
3 Matrix multiplication
Defining the matrix product is a two step process. First we will define what it
means to multiply a matrix
by a column vector and then we'll use that to tell us how two multiply matrices
in general. Let A be an
m ·n matrix and let v be an· n ·1 column vector (notice that the vector v has as
many entries as A has
columns). Write A in terms of its columns as above,
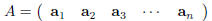
and write out the entries of v as

The product of A with v is defined to be
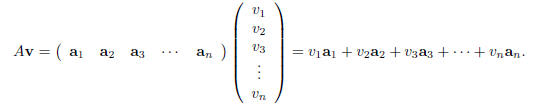
In words, we multiply the columns of A by the respective
entries of v and then add the results together.
According to this definition, the product of an m· n matrix and an· n ·1 column
vector is an m ·1 column
vector, i.e. the product is a column with as many entries as A has rows.
The process of multiplying a matrix by a vector is straightforward enough once
one is used to the
definition. Let's look at some examples. Suppose that we take
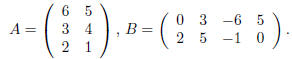
The matrix A can only be multiplied by column vectors with
2 entries while B can only be multiplied by by
column vectors with 4 entries. So, if we take
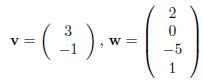
then
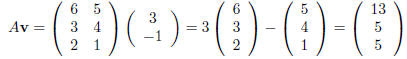
and
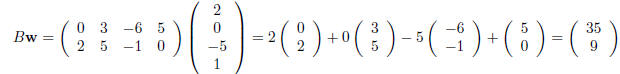
Since we can· now multiply matrices by (suitably sized)
column vectors, we can develop a way to multiply
matrices by other (suitably sized) matrices. Let A be an m· n matrix and let B be
a n ·p matrix. Notice
that B has as many rows as A has columns. In ·particular, the columns of B are n
·1 column vectors and
can therefore individually be multiplied by A. To be more specific, write B in
terms of its columns:
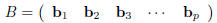
where each bj is an· n ·1 column vector. We define the
product of A and B to be
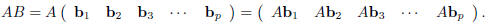
That is, to multiply two matrices simply multiply the first
matrix by the columns of the second and use the
results as the columns in a new matrix. Since each Aj is an m ·1 column vector,
and there are exactly p of
them, we find that AB is an m · p matrix.
Let's look at a quick example. Take
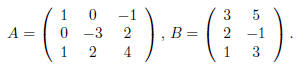
The product AB makes sense since A has as many columns as
B has rows. The definition of matrix
multiplication says that
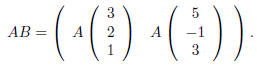
We find that
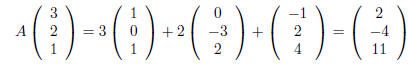
and
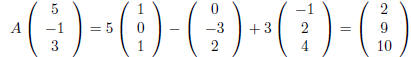
so that
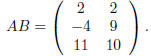
The n· n identity matrix I is the (square) matrix all of
whose entries are zero except for those along the
\main diagonal" which are all equal to 1. Symbolically
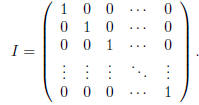
The  and
and
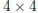 identity matrices are then
identity matrices are then
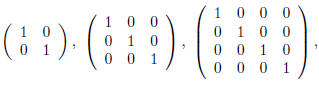
respectively.
The following theorem gives the main ·properties of matrix multiplication. These
all follow directly
from the definitions, but some are harder to prove than others, most notably that
matrix multiplication is
associative.
Theorem 2. Let A be m· n, B and C be n ·p, D be p· q, and let c be a real number.
Then
1. A(B + C) = AB + AC,
2. (B + C)D = BD + CD,
3. (AB)D = A(BD),
4. if I is the m m identity matrix then IA = A,
5. if I is the n· n identity matrix then AI = A,
6. c(AB) = (cA)B = A(cB).
4 Exercises
In exercises 1 and 2, let
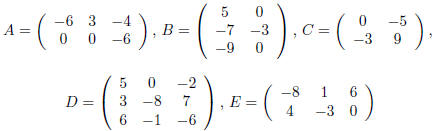
and compute each matrix sum or product if it is defined. If
it is not defined, explain why.
Exercise 1.
a. A - B
b. A - 3E
c. 2A + DB
d. AC
Exercise 2.
a. A + CB
b. 3BC - A
c. CAD
d. CA - E
Exercise 3. If 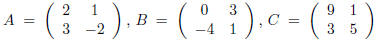 show
that AB ≠ BA but that
show
that AB ≠ BA but that
AC = CA.
Exercise 4. If 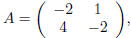 construct a nonzero
construct a nonzero
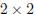 matrix
B (with two distinct columns) so that
matrix
B (with two distinct columns) so that
AB is the zero matrix.
Exercise 5. If A is an· n n matrix, we say the n· n matrix B is the inverse of A
if AB = BA = I,
where I is the n· n identity matrix. Show that if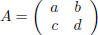 with
with 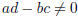 then the inverse of A is
then the inverse of A is
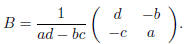
.
Exercise 6. If 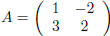 and
and
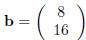 , use the inverse of A (see the previous
exercise ) to solve
, use the inverse of A (see the previous
exercise ) to solve
the matrix equation Ax = b for x.
Exercise 7. If 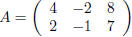 find a nonzero vector v so
that Av = 0.
find a nonzero vector v so
that Av = 0.



