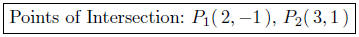8.13. Answer: The x-intercept of a function y = f(x) is the intersection
the graph of f and the x-axis. The x-axis is the graph of the
function g(x) = 0. Thus the x-axis is the intersection of two curves:
y = f(x) and g(x) = 0.
8.14. Solutions: Hopefully, you used standard procedures.
(a) Find points of intersection: f(x) = 6x + 3 and g(x) = 2x − 7.
When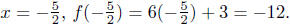 
Presentation of Answer: 
(b) Find points of intersection: f(x) = x + 3 and g(x) = 2 − 8x.
 |
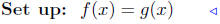equate ordinates |
 |
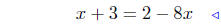substitute |
 |
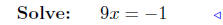add 8x − 3 both sides |
 |
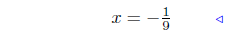divide by 9 |
When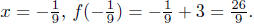 
Presentation of Answer: 
(c) Find points of intersection: f(x) = x2+7x−1 and g(x) = 4x−3.
 |
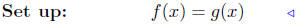equate ordinates |
 |
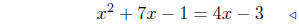substitute |
 |
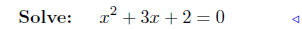add −4x + 3 both sides |
 |
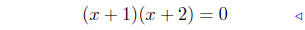factor |
 |
done! |
Calculation of Ordinates :
When x = −1, y = g(2) = −7.
When x = −2, y = g(3) = −11.
Presentation of Answer:
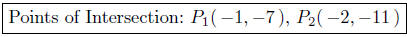
8.15. Solutions: We use standard procedures around here . . . how
about you?
(a) Find points of intersection: f(x) = 2x2−5x+2 and g(x) = x+3.
 |
equate ordinates |
 |
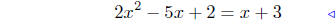substitute |
 |
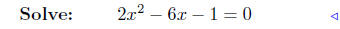add −x − 3 both sides |
 |
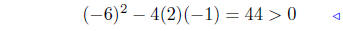pos. discrim. |
 |
Quadratic formula |
 |
|
These two curves intersect at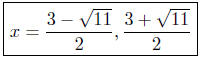 
(b) Find points of intersection: f(x) = x2 + 4x − 1 and g(x) =
1 − 4x − x2.
 |
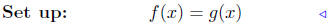equate ordinates |
 |
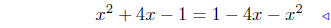substitute |
 |
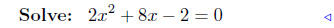add −1 + 4x + x2 |
 |
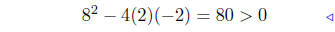pos. discrim. |
 |
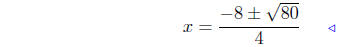Quadratic formula |
 |
|
 |
|
These two curves intersect at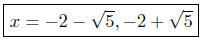 
(c) Find points of intersection: f(x) = 3x2 + 1 and g(x) = x2 − 5x.
 |
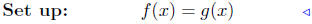equate ordinates |
 |
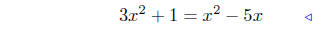substitute |
 |
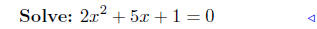add −1 + 4x + x2 |
 |
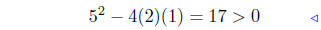pos. discrim. |
 |
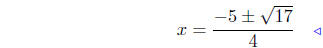Quadratic formula |
These two curves intersect at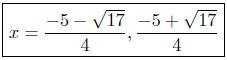 
8.16. Solutions: Follow the procedure.
(a) f(x) = 4x − 2 and g(x) = 4x + 12
 |
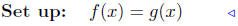equate ordinates |
 |
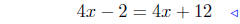substitute |
 |
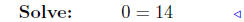add −4x + 2 both sides |
The equation 0 = 14 has no solution; i.e., no value of x can
satisfythe equation 0 = 14. Therefore, these two curves do not
intersect.
b) f(x) = 2x2 + 3 and g(x) = x2 − 1.
 |
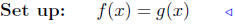equate ordinates |
 |
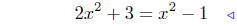substitute |
 |
add −x2 + 1 both sides |
The equation x 2 = −4 has no solutions; therefore, these two
curves do not intersect.
(c) f(x) = x2 + 2x + 2 and g(x) = x + 1
A negative discriminant (b2−4ac < 0) implies that the equation
has not solution; therefore, these two equations do not intersect.
(d) f(x) = x2 − 2x − 4 and g(x) = 4x2 − 3
 |
equate ordinates |
 |
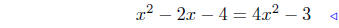substitute |
 |
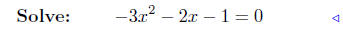add −4x2 + 3 |
 |
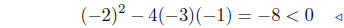negative discriminant |
A negative discriminant implies the equation has no solution.
Solutions to Examples
8.1. Solution:
P : (x1, y1) = (−2, 4)
Q : (x2, y2) = (3,−1)
We take the difference in the first coordinates and the difference in
the second coordinates.
x1 − x2 = −2 −3 = −5
y1 − y2 = 4− (−1) = 4+1 = 5
We now take the sum of the squares of these two:
(x1 − x2)2 + (y1 − y2)2 = (−5)2 + 52 = 25+25 = 50.
Finally, we take the square root of this result:
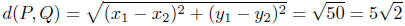
Presentation of Solution: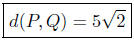 
Of course, this process can be accelerated once you fully understand
the computational steps.
8.2. Solution to: (a) Define f(x) = x2+3x+1. The natural domain is
the set of all real numbers for which the value of f(x) = x2+3x+1 can
be computed as a real number. For any real number x , the expression
x2 + 3x + 1 evaluates to a real number. Therefore, we deduce,
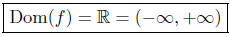
Solution to: (b) Define 
The numerator and denominator
always evaluate to a real number; however, if the denominator
evaluates to zero, the quotient is not a real number. Thus, we
can saythat
Dom(g) = { x | x2 − 3x + 2 ≠0}
This should not be considered to be a satisfactory characterization of
the domain of g though.
First find where x2 − 3x + 2 = 0, and reason from there. Solve
Therefore,
 |
|
 |
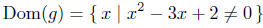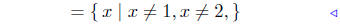set notation |
 |
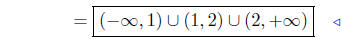interval notation |
Solution to: (c) Define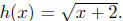 
For any x, x + 2 evaluates to
a real number, but for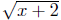
to evaluate to a real number we must
have x + 2 ≥ 0. Thus,
Dom(h) = { x | x + 2 ≥ 0 }
Again, we should not be satisfied with this formulation. We next solve
the inequality:
x + 2 ≥0 => x ≥ −2
Thus,
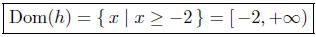
Solution to: (d) Define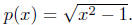 
In order for p(x) to evaluate
to a real number, we require x2 − 1 ≥ 0 and x ≠ 0. Thus,
Dom(p) = { x | x2 − 1 ≥ 0 }
We need to solve the inequality x2 − 1 ≥ 0. To do this, we use the
Sign Chart Method originallydiscussed in Lesson 7. (Actually, this
method reallyisn’t needed for this simple inequality. We could solve
as follows:
x2 − 1 ≥0 => x2 ≥1 => |x| ≥ 1,
but we shall use the Sign Chatr Method in any case, just to remind
you of this method.)
We begin by factoring completely the left-hand side (which is a difference
of squares):
(x + 1)(x − 1) ≥ 0
The Sign Chart of (x + 1)(x − 1)
Therefore, the solution to the inequality x2 − 1 ≥ 0 is
(−∞,−1 ] ∪ [ 1,+∞)
But the solution to this inequalityis the natural domain of p. Thus,
Notice how all the techniques of algebra (Lessons 1–7) are used:
factoring, solving inequalities, interval notation and so on.
This is the discouraging and challanging thing about mathematics :
To solve any given problem, we must call on our entire history of
experiences in mathematics. This is why it is so important for us to
try to master each of the little steps we take toward our final goals.
8.3. Solution: Consider
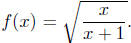Based on the above strategy,
we see that
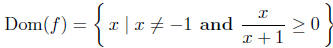
The first condition, x ≠ −1, avoids having zero in the denominator (we
exclude x = −1 from the domain); the second condition is necessary
for the radicand to be nonnegative. (The square root of a nonnegative
number is a real number, whereas the square root of a negative number
is a complex number . We don’t want to work with complex numbers
at this time.)
As you can see, I’ve simply translated the strategy into a series of
inequalities. We solve the inequality
first using the Sign Chart Methods.
The Sign Chart of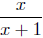 
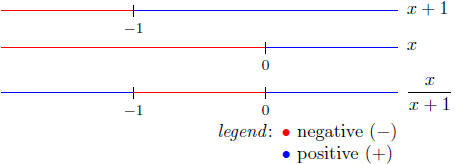
Therefore,
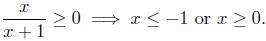
But, we also have the condition x ≠ −1; this changes the above solution
slightly to
x < −1 or x ≥ 0.
Presentation of Answer:
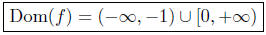
8.4. Solutions: We follow the standard procedures.
(a) Find the points of intersection of f(x) = 3x+2 and g(x) = 5x−4.
 |
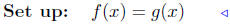equate ordinates |
 |
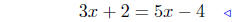substitute |
 |
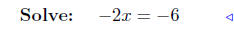add −5x − 2 to both sides |
 |
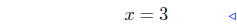divide by 3 |
At x = 3, f(3) = 3(3) + 2 = 11. Thus, ( 3, 11 ) is the point of
intersection.
Presentation of Solution: Intersection Point(s):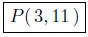
(b) Find intersection points of f(x) = x2−3x+1 and g(x) = 2x−5.
 |
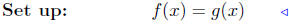equate ordinates |
 |
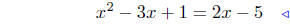substitute |
 |
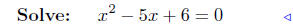add −2x + 5 both sides |
 |
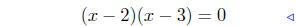factor |
 |
done! |
Calculation of Ordinates:
When x = 2, y = g(2) = −1.
When x = 3, y = g(3) = 1.
Presentation of Answer:
Points of Intersection:
