Notes on Factoring Polynomials in Two Variables

Let F be a field and consider 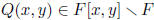. Our task is to factor
Q(x, y) into a product of irreducible polynomials.

Remark.

1. F[x, y] is a UFD.

2. Q(x, y) may be irreducible over F but may factor over some extension
field L/F.

Factoring a Polynomial in Two Variables

Step 0. Write 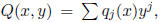compute the gcd of the 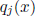, and
factor it out. WLOG 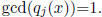So, content(Q) = 1 as a polynomial in
y with coefficients in F[x].

Step 1. Regard Q as a polynomial in y with coefficients in F(x). Take
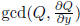to remove multiple factors.

Combining the previous two steps we can assume that Q has no factors
in F[x], and is square -free.

Step 2. Find 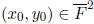with

and

The purpose of this is to find a point on the plane curve Q = 0 which
is non-singular and such that the tangent line at this point is not vertical.
This will allow us to write y as a power series in x. Now we justify the
existence of such a point before moving on to finding the power series.

Only finitely many points will satisfy the first equation in (* ) and not
the second. First, compute 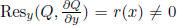(by step 1). We want
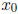such that 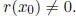(This 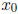may not be in F, but this is why we have
dealt with 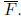.) Once we have found 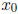, we can solve for 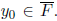One of
them will satisfy (* ).

WLOG assume 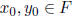, by extending F if necessary.

Step 3. Expand y as a power series: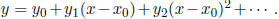
Now we use a recursive algorithm to compute 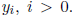(You may have
seen this as Newton’s algorithm or Hensel’s lemma). Suppos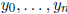e   are
known to satisfy



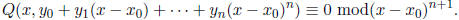
When n = 0,



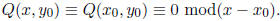
Now, for ease of notation, let
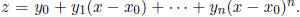
Then, for some b ∈ F, the induction hypothesis gives



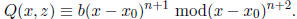
To find 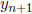, let 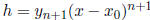and compute

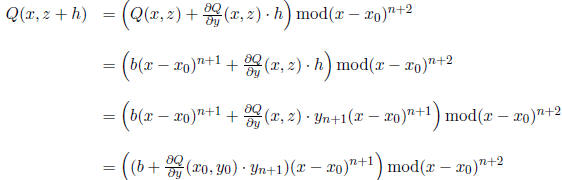
So, 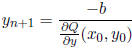does the trick. We now have our power series expansion
of y in terms of x . Use this method to compute y_n for
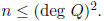
Step 4. For m = 1, 2, . . . ,deg Q; try to find P(x, y) ∈ F[x, y] of degree m,
starting with m = 1, with



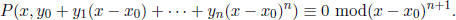
Stop if you find P, else go to next value of m . This is a system of linear
equations in the coefficients of P. So find the nullspace. If it is zero , go to
the next step.

Claim. The P of minimal degree m found in Step 4 is an irreducible factor
of Q.

Assuming the claim, then P | Q, so if Q ≠ P, we replace Q with Q/P
and repeat steps 2-4.

Why is the claim true? The point 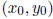about which the power series
expansion of y was given is on the plane curve Q = 0 and also on P = 0. The
conditions on P and Q ensure that the intersection multiplicity of P = 0
and Q = 0 at 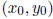is at least 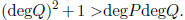Bezout’s theorem
then implies that P | Q.

Example. Let us illustrate with an easy example. Let Q(x, y) = x² − y².
Then 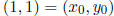  is a point on the curve Q = 0. And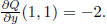
Expanding y in a power series: 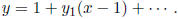We have

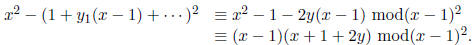
So, 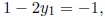giving .
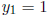Then, 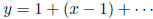. Now, find P of degree 1 satisfying

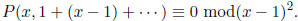
Say, P(x, y) = y − x, so P | Q.

A few weeks ago, we talked about how to factor in Z[x]. So, Q(Y )∈ Z[Y ].
The analogy here is between Z and F[x]. Find a prime p and a y0 such that

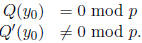
This is the same as finding 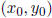. Now, use Hensel’s lemma: find
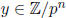
with 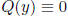mod pⁿ, for n large in relation to the coefficients of Q. Step
3 is to find the power series expansion of y:

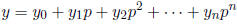
Now find P(Y ) ∈ Z[Y ] of small degree and with small coefficients such that
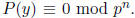(This can no longer be done with linear algebra .) This
congruence defines a lattice in 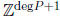. To find a short vector in a lattice,
there is an algorithm called the LLL-algorithm which we won’t explain.
Then a height calculation will replace Bezout to prove that P | Q.