N&0 – 20 Relative magnitude: Relative magnitude is
the property of relative size. It
refers to the relative size of numbers, objects, distances, brightness, and
other things that
can be quantified. The GLEs specifically require students to demonstrate
understanding
of the relative magnitude of different types of numbers by comparing, ordering,
and
identifying equivalent forms of numbers within and across number formats using
models,
number lines, equality (=) and inequality symbols (≠, ≤, ≥, >, <), and
explanations. (See
GLEs for specifics by grade.)
Table 1: Number Formats by Grade for Demonstrating
Relative Magnitude
(For grades K-1, consult your state’s Local GLEs.)
Grade |
Number Formats |
Within
Number
Formats |
Across
Number
Formats |
| 2 |
o Whole numbers 0 to 199 |
 |
|
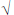| 3 |
o Whole numbers 0 to 999
o Positive fractions (halves, thirds, or fourths) |
|
|
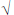| 4 |
o Whole numbers 0 to 999,999
o Positive fractions (halves, thirds, fourths, fifths, sixths, eighths,
or
tenths)
o Decimals (to hundredths place) |
|
|
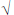| 5 |
o Whole numbers 0 to 9,999,999
o Positive fractions (halves, fourths, eighths, thirds, fourths, sixths,
twelfths, fifths, or powers of 10)
o Decimals (to thousandths)
o Benchmark percents (10%, 25%, 50%, 75%, or 100%)
o Integers in context |
|
|
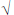| 6 |
o Numbers with whole number bases and whole
number exponents (e.g.,
34 compared to 43)
o Integers
o Rational numbers (fractions, decimals, whole number percents from 1 –
100%) |
|
|
| 7 |
o Numbers with whole number bases and whole
number exponents (e.g.,
34 compared to 43)
o Integers
o Rational numbers
o Absolute values
o Numbers in scientific notation |
|
|
| 8 |
o Numbers with whole number of fractional bases
and whole number
exponents (e.g., 34 compared to )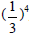
o Integers
o Rational numbers
o Absolute values
o Square roots
o Numbers in scientific notation
o Common irrational numbers (e.g.,  ,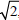
π ) |
|
|
N&0 – 21 Within number formats: To compare numbers
within number formats means
to compare whole numbers to whole numbers, fractions to fractions, decimals to
decimals , and so on.
N&0 – 22 Across number formats: To compare numbers
across number formats means
to compare whole numbers to fractions, fractions to decimals, decimals to
percents, and
so on.
Rational numbers: (See N&0 – 1.)
Whole Numbers: (See N&0 – 2.)
Positive fractions: (See N&0 – 3, N&0 – 4, N&0 – 5, N&0 – 6.)
Decimals: (See N&0 – 7.)
Percents: (See N&0 – 8.)
Integers: (See N&0 – 9.)
Real Numbers: (See N&0 – 11.)
Irrational Numbers: (See N&0 – 10.)
N&0 – 23 Absolute value: The absolute value of a
real number is the distance
between 0 and the number on the number line. The absolute value of a real number
x is
written as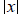 
. The absolute value of a
non- negative number (a number greater than or
equal to zero ) is the number (e.g.,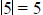 
since
the number 5 is a distance of five units
from on the number line). The absolute value of a negative number is the
opposite of the
number (e.g.,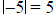 
since the number – 5 is five
units from 0 on the number line).
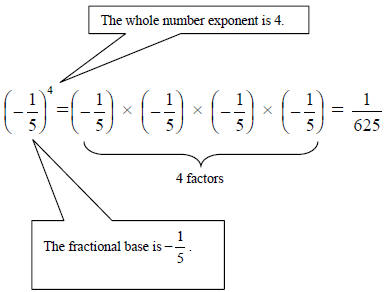
N&0 – 24 Whole number bases and whole number exponents,
and fractional bases
with whole number exponents: A whole number exponent is a whole number (See
N&O – 2) that indicates repeated multiplication of the same number. The
number being
multiplied is called the base. The exponent is typically written to the right of
the base and
slightly raised. The exponent indicates how many times the base is used as a
factor (See
N&O – 38).
Example 24.1 – Whole number base and whole number
exponent:
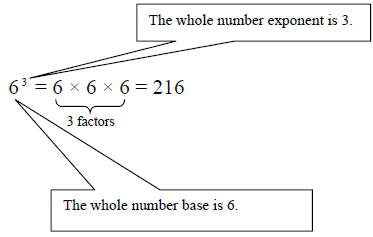
Example 24.2 – Fractional base with whole number
exponent:
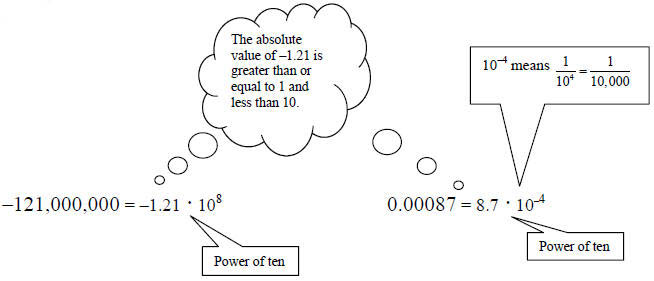
N&0 – 25 Scientific notation: Scientific notation
is a way of representing very large
or very small numbers as the product of a number , n, and a power of 10, where
the
absolute value of n is greater than or equal to 1 and less than 10.
Examples 25.1:
N&0 – 26 Ordering: Ordering numbers means placing
the numbers in numerical order
from the least to the greatest or from the greatest to the least.
Example 26.1:
Order the following numbers from the least to the
greatest: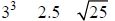 
Note: students may be asked to provide an explanation or place the numbers on a
number line.
Answer: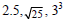 
N&0 – 27 Comparing: Comparing numbers, a and b,
means to determine if a is less
than b, if a is greater than b, or if a is equal to b.
Example 27.1: Alisa is placing
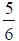on the number line below . Between which two
numbers should she place ?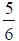
Answer: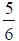 should be
placed between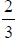
and 1 because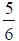is
greater than 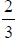and less than 1.
N&0 – 28 Number line: A number line is a line where
every real number corresponds
to a unique point on the line. Thus, if two numbers correspond to the same point
on the
line the numbers are equivalent (See N&O – 14).
Examples 28.1 – Horizontal number lines:
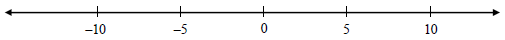
Example 28.2 – Using a vertical number line to locate
integers in context:
At what temperature is the arrow pointing?
Answer: The arrow is pointing at – 5°F.
