| Question: |
1 |
2 |
3 |
4 |
5 |
6 |
Total |
| Points: |
1 |
1 |
3 |
1 |
2 |
2 |
10 |
| Score: |
|
|
|
|
|
|
|
1. (1 point) Use the Euclidean algorithm to find GCD(23,
17).
__________________________________________________
__________________________________________________
______________________________________________________
_____________________________________________________
__________________________________________________
_______________________________________________________
2. (1 point) Suppose that x, y,m are integers, and 15x +
21y = z. What do you know
about z?
__________________________________________________
__________________________________________________
______________________________________________________
_____________________________________________________
__________________________________________________
_______________________________________________________
3. (3 points) What is the exponent of 3 in the canonical
decomposition of 50!?
__________________________________________________
__________________________________________________
______________________________________________________
_____________________________________________________
__________________________________________________
_______________________________________________________
4. (1 point) Suppose that x and y are integers. If GCD(x,
y) = 5, and LCM (x, y) = 210,
and x = 10, then what is y?
__________________________________________________
__________________________________________________
______________________________________________________
_____________________________________________________
__________________________________________________
_______________________________________________________
5. (2 points) Suppose that N is a large integer. Do you think there are more
primes
between 1 and N, or between N and 2N? Justify your reasoning with the prime
number
theorem:
__________________________________________________
__________________________________________________
______________________________________________________
_____________________________________________________
__________________________________________________
_______________________________________________________
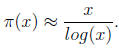
6. (2 points) Suppose that a, b,
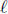∈ Z, and a, b ≠ 0. Define precisely what it
means to say
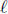that = LCM (a, b). In other words,
define the “ least common multiple ”.
__________________________________________________
__________________________________________________
______________________________________________________
_____________________________________________________
__________________________________________________
_______________________________________________________
