1. Suppose a, b, c ∈ Z.
(a) Show that if a|b and c ≠ 0, then ca|cb.
If a|b, then ax = b for some x ∈ Z, so cax = cb so (ca)x = (cb) i.e. ca|cb.
(b) Show that if a|b and b|c, then a|c.
If ax = b and by = c with x, y ∈ Z, then (ax)y = c = a(xy) so a|c since xy ∈
Z.
(c) Show that if a|b and a|c, then a|(mb + nc) for all m, n ∈ Z.
If ax = b and ay = c with x, y ∈ Z, then mb+nc = max+nay = a(mx+ny) so
a|(mb+nc)
since mx + ny ∈Z.
2. Show that there are arbitrarily long sequences of consecutive integers
containing no
primes. In other words, show that given an integer N ≥1, there exists an integer
a such
that a + 1, a + 2, . . . , a + N are all composites. Hint: try a = (N + 1)! + 1.
Look for an
“obvious” divisor of a + 1, an “obvious” divisor of a + 2 etc.
With a = (N + 1)! + 1, we have 2|2 and 2|(N + 1)! so 2|(a + 1) by Problem 1.
Indeed, for
2 ≤j ≤N + 1, (N + 1)! + j = a + (j − 1) is divisible by j because
j|j and j|(N + 1)!. On
the other hand, clearly each such j satisfies 2 ≤ j < a + (j − 1) so a + (j
− 1) cannot be a
prime, hence must be composite.
3. Suppose a, b, n are integers, n ≥1 and a = nd + r, b = ne + s with 0 ≤ r,
s < n, so
that r, s are the remainders for a ÷ n and b ÷ n, respectively. Show that r = s
if and only if
n|(a − b). [In other words, two integers give the same remainder when divided by
n if and
only if their difference is divisible by n.]
Suppose r = s. Then r = s = a − nd = b − ne. Rearranging the last two
equalities , we
get a − b = nd − ne = n(d − e) so n|(a − b). Conversely, suppose n|(a − b); we
will prove
that then r = s by contradiction. If r ≠ s, then switching r, s if necessary, we
can assume
without loss of generality that r > s. By assumption, n|(a − b). Thus, nx = a −
b for some
x ∈ Z so
a − b = nd + r − ne − s = n(d − e) + r − s = nx.
Rearranging the last equality we have r − s = n(d − e − x)
and d − e − x ∈ Z so n|(r − s).
Since r > s, we conclude that r − s ≥ n because the least positive multiple of n
is n itself .
But we have 0 ≤ s < r < n so r − s < n, a contradiction. We have thus shown that r
= s if
n|(a − b).
4. If n ≥2 and 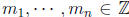 are n integers whose
product is divisibe by p, then at
are n integers whose
product is divisibe by p, then at
least one of these integers is divisible by p, i.e.
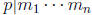 implies that
then there exists
implies that
then there exists
1≤ j ≤ n such that 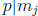 . Hint: use induction on n.
. Hint: use induction on n.
Proof by induction on n. Base case n = 2 was proved in class and in the notes as
a
consequence of 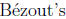 theorem.
theorem.
Induction step . Suppose k ≥ 2 is an integer such that whenever we are given k
integers
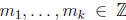 whose product is divisible by p (i.e.
whose product is divisible by p (i.e.
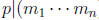 )), there exists
)), there exists
1≤ j ≤k such that p|mj . Now suppose we are given k + 1 integers
 such that
such that
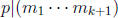 . We have
. We have 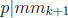 where
where 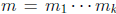 . By the base case, we conclude
. By the base case, we conclude
that either p|m or 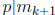 . If
. If
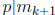 , then certainly there exists 1≤ j≤
k + 1 such that
, then certainly there exists 1≤ j≤
k + 1 such that
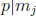 , namely j = k + 1. Otherwise, p|m and by
the induction hypothesis, then there exists
, namely j = k + 1. Otherwise, p|m and by
the induction hypothesis, then there exists
1≤ j ≤ k such that 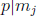 . Thus, we have shown that there exists 1 ≤j ≤k
+ 1 such that
. Thus, we have shown that there exists 1 ≤j ≤k
+ 1 such that
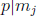 , completing the induction step . By PMI, we are done.
, completing the induction step . By PMI, we are done.
5. (a) Calculate gcd (315, 168) using the Euclidean algorithm, then use this
information
to calculate lcm (315, 168). Determine integers x, y such that 315x + 168y =
gcd(315, 168).
You may use the Blankinship version of the Bezout algorithm if you wish. Now
obtain the
prime factorizations of 315 and 168 to double -check your computation of the gcd
and lcm of
315 and 168.
To find gcd(315, 168), we perform the Euclidean algorithm, keeping track of what
it does
to the two extra columns comprising an “identity” matrix.
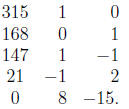
We read off that gcd(315, 168) = 21 (the last non- zero
remainder ) and that −1(315) +
2(168) = 21. We also have 8(315)−15(168) = 0 i.e. 8(315) = 15(168) and that
lcm (315, 168) =
8(315) = 15(168) = 2520. Or we could use lcm(315, 168) gcd(315, 168) = 315 ·
168.
To double-check, we have 315 = 32 · 5 · 7 and 168 = 23 · 3 · 7, so gcd(315, 168)
= 3 · 7 and
lcm(315, 168) = 23 · 3 · 5 · 7.
(b) Calculate gcd (89, 148) using the Euclidean algorithm.
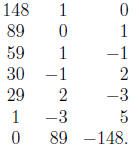
Thus, gcd(148, 89) = 1.



