An Algorithm for Computing Quotient and Remainder
Polynomials
ABSTRACT
The task of dividing one polynomial by another is encountered in continuous
fraction
expansion (CFE) and other engineering and systems science computations. This
note
presents an efficient algorithm for performing the division. A method for
constructing
synthetic division tableaus (SDT) for polynomials over any coefficient field is
formulated
and the relative ease in extracting the solution from the tableau is
demonstrated. The
beauty of the method lies in its simplicity even for manual calculations; and
above its
efficiency, a minimal memory space is needed for program execution. While other
programs and algorithms exist for performing this task, the algorithm introduced
in this
correspondence promises high efficiency and simplicity in formulation than many
of the
existing methods. To demonstrate its effectiveness and efficiency, the new
method is
compared to other existing methods.
I. Introduction
Polynomial long division (PLD) is often encountered in system science. It is
used for
computing the greatest common divisor of two polynomials . A description of the
operations of polynomial long division can be found in many texts on algebraic
computing. Most of these descriptions are simply extensions or direct
application of
Euclid’s algorithm. Also described in the literature is synthetic division
algorithm for
polynomials applicable only in the case of a first order denominator (devisor)
polynomial. PLD operations have been implemented in several different algebraic
programs, over the years, with varying efficiencies and computer memory
requirements.
Examples of softwares (old and new) with PLD operations include Altran, Derive,
Macsyma, MathCad , Mathematica, Maple, Reduce , SAC, and SMP.
The purpose of this correspondence is to introduce a novel algorithm for
polynomial long
division which is comparable to the Euclidean in efficiency, if not superior. It
is
applicable to polynomials of any degrees and over any coefficient field. This
new
algorithm also requires minimal memory space and thus will be as useful as
existing
operations for computer program implementation. Perhaps the most attractive
features of
the proposed algorithm are its conceptual simplicity and convenience for
calculations.
This paper constructs a PLD tableau based on a pattern of
relationships between the
operands in a long division process. An algorithm for constructing the tableau
is
described. An algorithm for constructing the tableau, the termination criterion
and
interpretation of results are described. An example is used to illustrate the
application of
the proposed algorithm.
II. Formulation of Algorithm
Consider two polynomials in s,
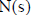 and
and
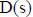 over a field, given by:
over a field, given by:
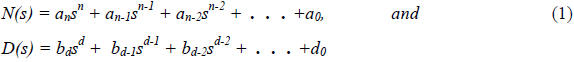
Where d > or = n.

It can be shown that the quotient polynomial
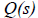 is of
the form:
is of
the form:
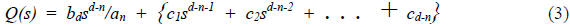
and the remainder polynomial
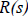 is given by:
is given by:
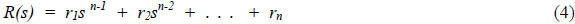
A tableau can be constructed from which the coefficients
 of
of 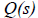 and
and 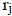 of
of 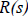 are
are
obtained. The first two rows of the tableau are formed by the coefficients,
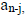 of
of 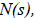
the divisor - first row, and the coefficients 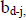 of
of 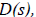 the dividend - second row;
the dividend - second row;
j = 0,1,2,…d. Elements of subsequent rows of the tableau are derived from the
determinants of 2x2 matrices formed from an array of the first and last rows. In
addition
to the rows formed with the coefficients of the divisor,
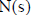 - the Pivot row, and the
- the Pivot row, and the
coefficients of the dividend, 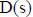 defined
as ‘row zero’, d-n+1 rows are generated. Thus
defined
as ‘row zero’, d-n+1 rows are generated. Thus
the synthetic division tableau so formed is a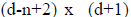 matrix. This format is
matrix. This format is
illustrated in Table 1. below.
Table 1. Format for Synthetic Division Tableau
| Description |
j=0 |
j=1 |
j=2 |
… |
d |
| PIVOT ROW: a n-j |
an |
|
|
|
0 |
| ROW ZERO: bb-j t=0 |
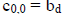 |
|
|
|
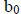 |
| t=1 |
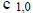 |
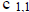 |
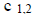 |
|
|
| t=2 |
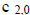 |
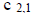 |
|
|
|
| . |
|
|
|
|
|
| . |
|
|
|
|
|
| t=d-n |
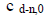 |
|
|
|
|
REMAINDER COEFFICIENT ROW:
t=d-n+1 |
|
|
|
|
|
Based on the above row definitions, equation (3) simply
becomes
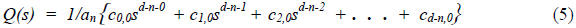
Where 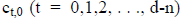 represents the ‘row t,
column zero’ element (entry) on the
represents the ‘row t,
column zero’ element (entry) on the
tableau. Also, the entry 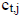 on the tableau is given by
on the tableau is given by
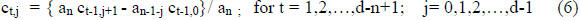
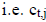 are calculated using the pivot row and the last
row.
are calculated using the pivot row and the last
row.
The following postulates are useful for determining the termination of the
algorithm and
for obtaining the results from the tableau:
(i) 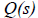 has d-n+1 possible terms
has d-n+1 possible terms
(ii) 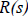 has n terms
has n terms
(iii) The coefficient of the 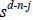 term in
term in
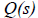 is
is
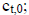 for t = j = 0,1,2,…d-n
for t = j = 0,1,2,…d-n
(iv) The coefficient of the 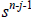 term in
term in
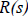 is
is
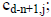 for j = 0,1,2…n-1.
for j = 0,1,2…n-1.
Thus we observe that once the tableau is constructed the quotient polynomial can
easily
be assembled from the first row, j=1, and the coefficients for the remainder
polynomial
are simply the elements of the last row, t=d-n+1, and in descending power of the
variable .
III. Illustrative Example
To illustrate the proposed algorithm, we consider the division
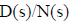 of the
following
of the
following
pair of Polynomials given by:
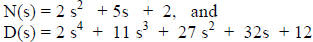
d = 4, n = 2, the order of
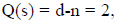 the order of
the order of
 and the number of
and the number of
steps = d-n+1 = 3; t = 0,1,2,3.
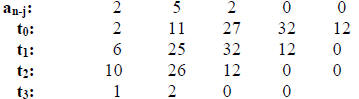
Hence,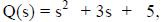 and
and

IV. Concluding Remarks
A nontrivial algorithm for finding the quotient and remainder polynomials is
derived. It
will be noted that the algorithm requires an explicit division only by an the
leading
coefficient of 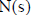 and it should also be observed that there are only d–n+1
steps required
and it should also be observed that there are only d–n+1
steps required
in the computation of the coefficients of
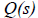 and
and
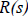 . In these regards this
algorithm is
. In these regards this
algorithm is
similar to the Euclidean and since there are no loops or recursions in this
algorithm it
might be more efficient than most long division process described in algebraic
texts .



