An Introduction to Partial Differential Equations in the Undergraduate Curriculum

1.5. The Transport Equation

One of the driving motivations for studying PDE’s is to describe the
physical world around us. We can use a flux argument to derive
equations describing the evolution of a density, which is just a fancy
word describing the concentration of something (mass in a region, heat
in a metal bar, traffic on a highway) per unit volume.

Consider a one-dimensional freeway and let 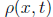be the density
of cars per unit length on the freeway.

Figure 1.1: Flux argument for cars on a freeway.
( draw your own figure).

Then the mass of cars in the region a < x < b is given by

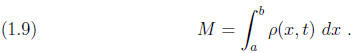
Now suppose we are measuring the flux, Q, of cars into this region
measured in mass/unit time. It can written in terms of the number of
cars crossing into the region at x = a, called q(a), minus the number
of cars that flow out of the region at x = b, called q(b),

Now, by conservation of mass, the rate of change of the mass between
a and b is given by the flux into the region,

We can rewrite the flux by a clever application of the fundamental
theorem of calculus:

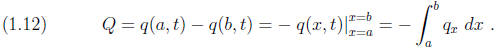
We can now rewrite the conservation of mass equation as

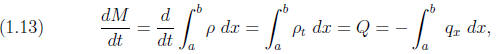
or, rearranging

Since this is true for every interval a < x < b, the integrand must
vanish identically. So

Equations of this form are called transport equations or conservation
laws – they are a very active area of study in PDE’s.

We can propose a simple model for the flux function q(x, t) – suppose
we assume the cars are all moving at a constant speed C. Then
we can argue that the flux is just equal to the product of the number
of cars time the speed they are moving at,

Substituting into the transport equation yields

which is just the convection equation. If we specify the initial distribution
of cars,

we can show fairly easily that the solution to the convection equation
with this initial condition is just

corresponding to cars moving uniformly to the right.

Physically, we just see the distribution of cars translating to the
right with a speed of C.

Figure 1.2: Solution to the convection equation.
( draw your own figure).

To verify this solution let 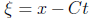, and look for a solution .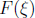
Then, by the chain rule

Substituting 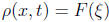into the convection equation (1.17), we find

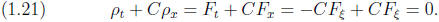
Moreover, when t = 0, we find 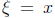so that the initial condition
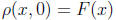is satisfied also.

1.6. Challenge Problems for Lecture 1

Problem 1. Classify the follow differential equations as ODE’s or
PDE’s, linear or nonlinear , and determine their order. For the linear
equations, determine whether or not they are homogeneous.

(a) The diffusion equation for h(x, t):

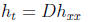
(b) The wave equation for w(x, t):

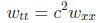
(c) The thin film equation for h(x, t):

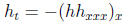
(d) The forced harmonic oscillator for y(t):

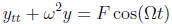
(e) The Poisson Equation for the electric potential :

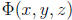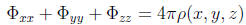
where 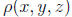is a known charge density.

(f) Burger’s equation for h(x, t):

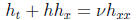
Problem 2. Suppose when deriving the convection equation, we assumed
the speed of the cars was given by βx for x > 0.

(a) Explain why the flux function now is given by
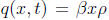
and the associated transport equation is given by

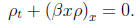
(b) Explain why

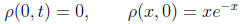
correspond to a boundary condition of no flux of cars in from
the origin and an initial condition specifying the distribution
of cars at t = 0.

(c) Verify that

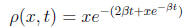
is a solution to both the transport equation given in (a) and
the initial and boundary conditions given in (b).

Problem 3. Show that the helicoid

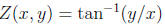
satisfies the minimal surface equation,

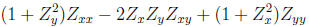
MAPLE may be helpful with the algebra .

Problem 4. Show that the soliton

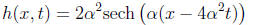
satisfies the the Korteweg-deVries equation,

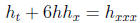
MAPLE may be helpful with the algebra , in particular if you don’t
remember your hyperbolic trigonometric identities .