since the Otter Creek Observatory is being renovated, this might be a good
time to
talk about telescope design. The thrust of our current renovation progress is
really
‘retro’ in that we are incorporating a traditional instrument design by adopting
a
high-quality, long-focus refractor in our equipment suite. Come with us as we
take a
brief tour of some of the various types of telescopes to get an overview of the
variety of
instruments used to process light as it comes to us from space.
Telescopes are instruments that process light signals from the Sun , Moon, and
planets
and of course, from the stars themselves. The first telescopes were “refractors”
--
telescopes that process light by refracting (bending) it with lenses. All
refractors have
the basic design shown below -- the telescope design that most people probably
think of
when they think “telescope”. The “objective lens”, A, receives the light
transmitted from
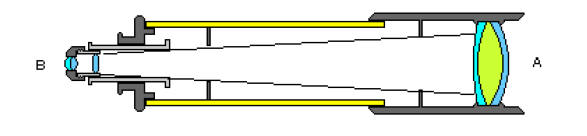
a source like a planet , star or some terrestrial object like a tree. The
image is focused to
an “eyepiece lens”, B. The eyepiece brings the image to a final focus where an
observer
can actually see the object that the telescope is
pointed toward. Galileo was one of the first to use
such an instrument to observe the Moon and
Jupiter and its satellites. The refractor was
developed because of eyeglasses! Eyeglasses
use a lens to bend light so as to improve people’s
vision. Around the time of Galileo people
discovered that the lenses used in eyeglasses
could be combined to produce a device that would make objects appear closer --
the
device which we now call a refracting telescope.

Refractors have the nice feature that little light is lost in the process of
refraction. One
big problem with refractors used to be color distortions, so that red and blue
fringes
would appear around objects giving a false impression of the true colors of the
object.
Opticians improved the quality of objectives over time. Today, very high-quality
objectives, called apochromatic lenses, are routinely engineered. They are
considered
by some to be as near to telescope perfection as one can get . The downside to
these
lenses is that they are quite expensive.
Another big development in telescope design came during the 17th century with
the
notion of taking light and reflecting it to a focus with a mirror rather than
refracting it with
a lens. In this design the light enters an open tube at A as shown below, passes
through
the tube to a concave mirror, called the “primary” mirror, at B. The mirror then
does the
job of focusing the light rays to a flat “secondary” mirror which bounces the
rays at a 90
degree angle up to an eyepiece at C. An observer looks down through the eyepiece
and
sees the image.

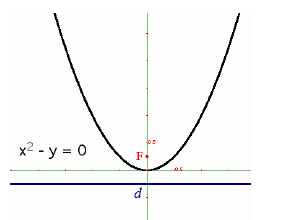
The curve of a reflector ’s mirror is similar to the curve
of satellite TV dishes. The principle of focusing
radiation this way is the same for both. The
mathematics and design is fairly simple. In fact, if you
have ever taken an algebra course , you probably had
to suffer through graphing a parabola like this one .
The curve of the mirror in a modern reflector is a
parabola -- albeit not as
deep as this parabola
shown. Isaac Newton, who
invented the reflector, actually used a telescope (pictured at
left) in which the curve of the mirror was just a segment of a
simple circle . However, the parabolic shape produces better
images than does the simple circular (or “spherical”) shape.
This earliest type of reflector is called a “Newtonian” reflector.

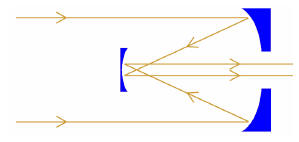
Another early reflector
design was the
“Gregorian” design, in
which the secondary
mirror was concave and
reflected light back through a hole in the primary
mirror. The early reflectors caused a stir because their tubes were noticeably
shorter
than refractors of the same aperture (width) while providing reasonably good
images,
and shorter telescopes were easier to handle.
From this point, we begin to see an ever widening
diversification of types of reflecting
telescopes. For one, during the eighteenth century, Sir William Herschel
experimented
with the existing design of the reflector to modify the location of the
secondary mirror. In
the Newtonian and Gregorian designs this mirror is actually located directly in
the path
of incoming light. In what became known as the “Herschelian” type reflector,
the primary mirror, A, would be tilted at a slight angle (τ) and the secondary
mirror, B,
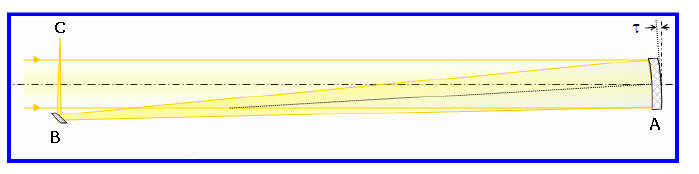
was removed further to the side of the telescope out of
the path of the incoming light.
This design is the first example of what has become known as “off-axis”
reflectors, so-
named because such telescopes reflect their light askew with respect to the
optical axis
of a traditional Newtonian reflector. It is also an “unobstructed” reflector
because the
light path is not obstructed by the secondary mirror.
Yet another design took the light path through the primary
mirror in a manner somewhat
like the Gregorian. This form, known as the “Cassegrain” reflector, bounces
incoming
light off the concave primary mirror at B, as before. But now, the light is
returned back
via a convex secondary mirror at C, to pass back through the primary via a hole.
An
eyepiece at D focuses the image for viewing.
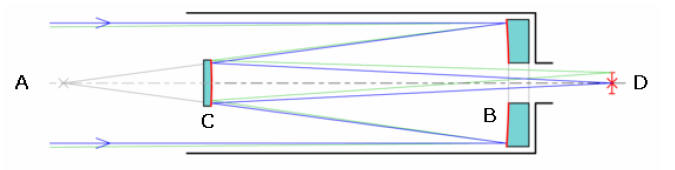
The Cassegrain had the advantage that it duplicated the
long focal length (the distance
the light travels between the mirror and the focus) of refractors without the
long tube
that was necessary for refractors. Long focal lengths are good for producing
high
magnifications desirable for viewing the planets, moon, and close groupings of
stars .
Unfortunately, there were image distortions that needed to be remedied, but this
instrument led to a line of designs called folded-optic reflectors, because as
the name
implies, the light path is folded back on itself.
Two main variants of the Cassegrain design were
developed to deal with image distortions in different
ways. One design, called the Schmidt-Cassegrain has
been widely popularized by telescope manufacturers
like Celestron and Meade. This design uses a special
corrector plate (P) on the incoming light to correct for distortions. The
secondary mirror
is attached on the back side of the corrector plate. A similar design called the
Maksutov
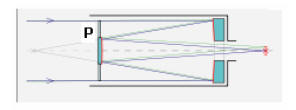
employs a more curved corrector plate and a spherical
primary mirror. Other designs
involve the same basic concepts but again, modify the type of curvature of the
primary
and secondary mirror and the type of correcting plates used. Such designs are
all
known as “catadioptric” -- a term applied to instruments which employ both
lenses and
mirrors. Continuing in this vein, Maksutov’s designs were coupled with the
classical
Cassegrain to produce a Maksutov-Cassegrain and also with a traditional
Newtonian to
produce a Maksutov-Newtonian. Essentially, the difference between these types of
catadioptrics and those involving the Schmidt designs are in the shape of the
correcting
plates.
A separate branch of instruments uses two or more mirrors
of different geometric
configurations, such as elliptical or hyperbolic, in some combination. In this
branch
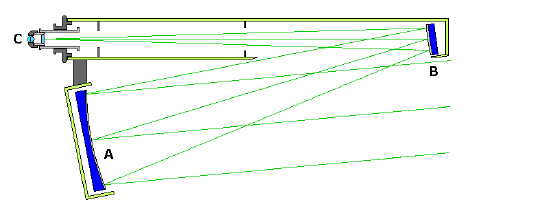
some very unusual designs have evolved. Among these are the schiefspieglers,
which
in German means a “skewed” or “oblique” reflector design. Essentially, these
variants
go to sometimes great lengths to produce a reflector that is both compact and
unobstructed. One such design is shown below.
Well, we have taken a quick, although by no means
exhaustive, tour of the development
of some telescope designs. Each new design presented advances in solving
problems
of some preceding type, but usually requiring some additional expense or
tradeoff.
When the observatory’s renovation is complete, Otter Creek Observatory will
feature
telescopes of both the refractor and Schmidt-Cassegrain designs. We hope you
will
come see them.



