Basic Calculus with Applications

2.2: Limits and Continuity

• If you can easily sketch the graph of a given function, it is easy to classify points of
continuity and/or discontinuity. Refer to the examples we discussed in class.

• Definition of Continuity

Let c be a number in the interval (a, b), and let f be a function whose domain contains
the interval (a, b). The function f is continuous at the point c if the following
conditions are true.

(a) f(c) is defined.

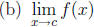exists.

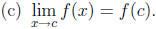
• Continuity of Polynomial and Rational Functions

o A polynomial function is continuous at every real number .

o A rational function is continuous at every number in its domain.

Example 1: Let f(x) = x³ + 2x + 2 and

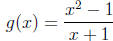
o Since f is polynomial, it is continuous at every point.

o Since g is a rational function with domain all real number but x = -1, it is continuous
everywhere except at x = -1.

Example 2: Given

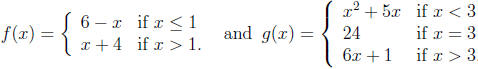
• f(x) is continuous at every point including at x = 1 (Why?)

• g(x) is continuous at every point except at x = 3 (Why?)

3a. Relative extrema

• Definition of Critical Points of f:

A critical point of a function f is a point in the domain of f where f'(x) = 0 or f'x)
does not exist.

Example Given f(x) = x² - 2x and .
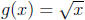Obviously, f'(x) = 2x - 2 and .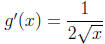

Since f'(1) = 0, x = 1 is its critical point, and since g'(0) does not exist, x = 0 is its
critical point.

• Revise the definition of relative extrema (relative maximum, relative minimum).

• We classify the critical points as local maximum, local minimum, or neither. Let x = c
be the critical point of a function f.

o When we go from left to right of x = c, if the sign of f ' changes from positive (+)
to negative (-), then f has a relative (local) maximum at x = c.

o When we go from left to right of x = c, if the sign of f' changes from negative
(-) to positive (+), then f has a relative (local) minimum at x = c.

o If there is no change in sign, then x = c is neither a relative minimum nor a relative
minimum.

Example: Given f(x) = x³, which is differentiable for every real number x.

Since f0(x) = 3x², x = 0 is its only critical point. However, the sign of f' does not
change its sign. Thus x = c is neither a local minimum nor a local maximum.

3b. Finding the absolute maximum and minimum on a closed interval

• If f is a continuous function on a closed interval I = [a, b], then f has an absolute
minimum and absolute maximum on I.

In this case, it helps to follow the following steps to find the absolute minimum and
absolute maximum.

Step 1 Find the critical points (if any) of the function f. Take only those critical points
that are in the interval I.

Step 2 Compute f(a), f(b), and the the value of the function at those critical points
found in Step 1.

Step 3 Compare the quantities found in Step 2; the greatest and the smallest of the
quantities are the maximum and the minimum of f, respectively.

3c: Sketching the graph of a function

• Once you correctly found the critical points and carefully classified them as local max-
imum, local minimum, you should be able to sketch the graph of the function. Make
also sure to find the y- intercept. If you can, find the x- intercepts, too.

Example:

3d: Optimization Problems

• One of the most common applications of calculus is the determination of the optimum
(minimum or maximum) values.

• Here are suggested guidelines for solving Optimization Problems.

1. Identify all given quantities and all quantities to be determined, also called the
unknown(s). Draw and label a diagram as needed.

2. Identify the quantity to be minimized or maximized, also called the objective func-
tion.

3. Using the given condition, reduce the objective equation to one having a single
independent variable.

4. Determine the feasible domain of the objective function.

5. Find the absolute maximum or minimum of the objective function.

3e. Related Rates Problems
• Recall that if Q is a quantity changing over time, then the derivative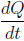 is the rate
at which Q changes over time.

• In related rates problem, we have two (sometimes more) related quantities, we know
the rate at which one is changing, and we wish to find the rate at which another is
changing.

• Strategy for Solving Related Rates

o Case 1. If the equation relating the quantities is given, use the following strategy.

1. Use Chain Rule to differentiate both sides of the equation with respect to t.

2. Substitute the given information into the resulting equation and solve for the
unknown rate.

Example 1: A point is moving along the curve

y = x³ + 2x

in such a way that its x- coordinate is increasing at the rate of 5 unit per second. How
fast is its y- coordinate changing when x = 2?

Solution : In this example, we are given that 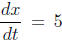. We want to find 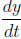when
x = 2.

Now, differentiating both sides of the equation y = x³ + 2x, we obtain

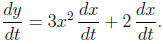
Substituting the given condition, we have

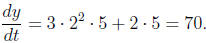
Therefore, the y- coordinate is increasing at the rate of 70 units per second.

o Case 2. If the equation relating the quantities is not given, use the following strategy.

1. Read the problem carefully. Draw a diagram if possible.
2. Introduce notations. Assign symbols to all quantities that are functions of time.
3. Express the given information and the required rate in terms of derivatives .
4. Write an equation that relates the various quantities of the problem.
5. Use the Chain Rule to differentiate both sides of the equation with respect to t.
6. Substitute the given information into the resulting equation and solve for the
unknown rate.

Example 2: The radius of a circle is increasing at a rate of 10 cm/sec. How fast is
the area increasing at the instant when the radius has reached 5 cm?

Solution: In this example, unlike example 1, the equation relating the two quantities
(the radius and the area) is not given.

Now let r be the radius and A be the area of the circle , respectively.
We are given that 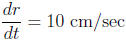. We want to find 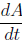when r = 5 cm.

The equation relating the changing quantities r and A is

A = πr².

Differentiating this equation with respect to t and substituting the given quantities,
we obtain

• For more problems on related rates, refer to the practice problems and the lecture
notes of 04/21/06 and 04/24/06.

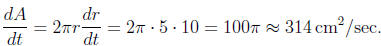
4a: The Indefinite Integral

• A function F is an antiderivative of a function f if for every x in the domain of f, it
follows that F'(x) = f(x).

Example: In each of the following, assert that F'(x) = f(x).

o The antiderivative of f(x) = 2x is F(x) = x².
o The antiderivative of 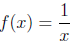is F(x) = ln x.

o The antiderivative of f(x) = e^x. is F(x) = e^x

• Every antiderivative F of f must be of the form F(x) = G(x) + C, where C is a
constant.
• The expression 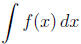read \the indefinite integral of f with respect to x," means
to find the set of all antiderivatives of f. In addition , f is called the integrand, and x
is the variable of integration .

• Some Integration Rules
1. Constant Rule. .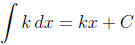
2. Constant Multiple Rule .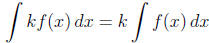

3. Sum Rule . .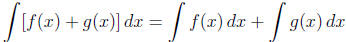
4. Power Rule (r ≠ -1) .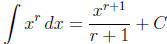
5. Power Rule (r = -1). 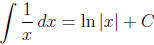.