Cardinality and CoCardinality and Countablility

I thought I’d write up what we did in class, plus give you some additional notes and
exercises having to do with cardinality and countablity. I’ve modified the countability
definition slightly ( but equivalently ) to use Z⁺ = {1, 2, 3, 4, …} instead of
N = {0, 1, 2, 3, ….}, because that’s more standard. The proof that the two definitions are
equivalent is Exercise #2. Note: I’ve numbered all the definitions , examples and
theorems sequentially. Also, it’s best to view this file in color, since color is used to
clarify some proofs.

Definition 1. Two sets A and B have the same cardinality if and only if there is a one-to-
one correspondence (i.e., a bijection) between A and B. In other words, A and B have
the same cardinality if and only there is a bijective function f: A -> B (or equivalently, a
bijective function g: B -> A).

Definition 2. A set S is countably infinite if there is a bijective function f: Z⁺ -> S. A
set that is either finite or countably infinite is called countable. A set that is not
countable (i.e., neither finite nor countably infinite) is called uncountable.

Example 3: The set S = {2, 4, 6, 8, …} is countably infinite, and hence countable,
because f: Z⁺ -> S, with f(n) = 2n, is a a bijection.

Theorem 4. The set of real numbers R is uncountable.

Proof by contradiction. Suppose not, i.e., assume that there is a bijective function
f: Z⁺ -> R. Since every real number has a decimal expansion, we can then create a list
of all real numbers (a finite decimal expansion will be filled out with zeroes, e.g. 0.5 =
0.5000…). For example, making up some values for f , the beginning of our table might
look like this :

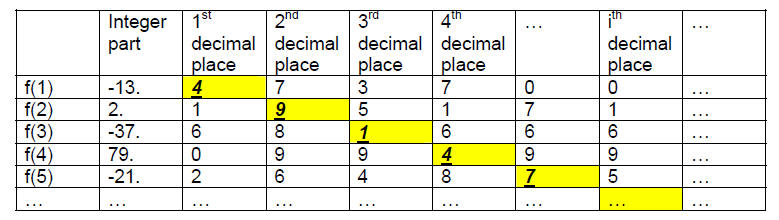
We now define a number x (slightly differently than in class , since I’m using Z⁺ instead
of N), that cannot appear in the table, since its decimal expansion differs from each f(i)
in the i^th decimal place:

x = 0.x₁x₂x₃x₄…, where, if the i^th decimal place of f(i) is 4, then x_i = 3; otherwise x_i = 4. In
our example above, the first few digits of x are x = 0.34434…. Since x always differs
from f(i) in its i^th  decimal place, x ≠ f(i) for any i, and we have contradicted the
assumption that we were able to construct the bijective function f. Therefore we
conclude that R is uncountable.

Remark 5. A very handy way to think of a countable set is as one whose elements can
be listed in a sequence, finite or infinite, since a sequence of the form {s₁, s₂, …, s_n}
(i.e., finite) or {s₁, s₂, …, s_n, ...} (i.e., infinite) is, as discussed in class a function, either
f:{1, …, n} -> S, or f: Z⁺ -> S. If f is a bijection to S, then by Definition 2, S is countable (in
fact, if and only if f is a bijection to S).

For instance, in Example 3, writing the set of positive even numbers in the sequential
way S = {2, 4, 6, 8, …} is implicitly giving the bijection: {2 = f(1) = s₁, 4 = f(2) = s₂, 6 =
f(3) = s₃, …}. Many times it’s convenient to use this formulation of countability in proving
a theorem: “Suppose S is countable. Then the elements of S can be listed in a finite or
infinite sequence, S = {s₁, s₂, s₃, …}.”

Here is a second amazing theorem (the first being Theorem 4) that I mentioned in class,
but did not prove:

Theorem 6. The set Q⁺ of positive rational numbers is countably infinite.

Proof. We begin by listing all possible fractions of the form p/q in a matrix, with one row
for each possible value of p = 1, 2, 3, …, and one column for each possible value of
q = 1, 2, 3, … (the arrows and shading in the diagram are explained below):

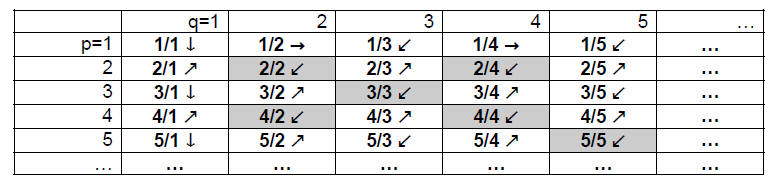
Note that all positive rational numbers must appear somewhere in the table, because
every positive rational number can be written in the form p/q, where p and q are positive
integers. In fact the rational number p/q will appear infinitely many times , as p/q,
2p/(2q), 3p/(3q), …. We use this table to get a sequential listing of Q⁺ by doing two
things:

• Traverse the table in the “zig-zag” manner indicated by the arrrows 
starting with 1/1. Note that eventually we visit every number in the table.

• Once you put a number on the list, skip any others that equal it – e.g., list 1/1, but
don’t list 2/2, 3/3, 4/4, …. Among the numbers listed in the partial table above, I’ve
marked in gray the boxes that contain the duplicates that should be omitted from the
list:

Traversing the table in the order above , and listing numbers only the first time we see
them, we get the following sequential listing of Q⁺:

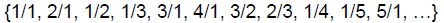
Thus Q⁺ is a countably infinite set!

The next two corollaries follow from Theorems 4 and 6. Their proofs are Exercise #4.

Corollary 7. The set Q of all rational numbers is countably infinite.
Corollary 8. The set R-Q of all irrational numbers is uncountably infinite.

Together, Corollaries 7 and 8 say there are way more irrational numbers than rational
numbers!

We’ve defined what it means for two sets to have equal cardinality, but we can also
define what it means for one set to have bigger or smaller cardinality than another.

Definition 9. We denote the cardinality of a set S by |S|. If S and T are any two
nonempty sets, we say that |S| ≤ |T| if there is a one-to-one function from S to T. For
any set T we define |Ø| ≤ |T|.

If S and T are finite sets, then |S| ≤ |T| means that S has at most the same number of
elements as T, since the range of a one-to-one function from S to T is a subset of T that
has the same number of elements as S. It’s also clear, if S and T are both finite, that |S|
= |T| if and only if |S| ≤ |T| and |T| ≤ |S|. Intutively, this may also seem true for infinite
sets, and it is indeed true, but it’s not so easy to prove that. In other words, if S and T
are two infinite sets, suppose we have a one-to-one function f: S -> T (so |S| ≤ |T|), and
we have a one-to-one function g: T -> S (so |T| ≤ |S|). How can we use f and g to
construct a bijection h: S -> T, proving that |S| = |T|? I’ll state the theorem, but I’ll omit its
proof (which is very cool, by the way) – if you’re interested in the proof, ask and I’ll give
you a reference.

Theorem 9 (Schroeder-Bernstein Theorem). Suppose S and T are two sets, with |S| ≤
|T| and |T| ≤ |S|. Then |S| = |T|. In other words, if there exist one-to-one functions
f:S -> T and g: T -> S, then there exists a bijective function h: S -> T.

If |S| ≤ |T|, but |S| ≠ |T|, then we write |S| < |T|, The last thing I’ll include is a theorem
that says that, for any set S, |S| < |P (S)|. Its proof is Exercise #5.

Theorem 9. If S is any set, |S| < |P (S)|.

Corollary 10. There exist an infinite number of sets, any two of which have different cardinality.

Proof of Corollary. Let S₁ = Z⁺, and for each n > 1, let S_n = P (S_n-1). In other words, S₂
= P (Z⁺), S₃ = P (P (Z⁺)),S₄ = P( P( P (Z⁺))), etc. By Thm. 9, |S_n| < |P (S)_n+1| for all n.

Exercises

1.
a. Show that the set of positive odd integers is a countable set.
b. Show that the set of all odd integers, positive or negative , is a countable set.

2.
a. Show that Z⁺ and N have the same cardinality by constructing a bijective
function f: Z⁺ -> N.
b. Suppose S is a set. Using the function f from part (a), and/or its inverse
function f^-1, prove: There is a bijection g: N -> S if and only if there is a
bijection h:Z⁺ -> S. This proves that the definition of countability given in class
is the same as the one in Definition 2.

3. Use the “sequential” formulation of countability given in Remark 5 to prove: If S and
T are both countable sets, then S 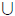T is a countable set.

4. Both parts of this exercise make use of the results of Theorem 6 (Q⁺ is a countable
set) and exercise 3 (the union of two countable sets is countable).
a. Prove that the set Q of all rational numbers is a countable set.
b. Prove that the set R - Q of irrational numbers is an uncountable set.

5. Parts (a) and (b) of this exercise together comprise a proof of Theorem 9.

a. Let S be any nonempty set. Construct a one-to-one function from S to P (S),
which proves that |S| ≤ |P (S)|.

b. Let S be any nonempty set. Prove that there is no bijection from S to P (S), by
completing the following proof by contradiction: Suppose there is a bijection
f: S -> P (S), i.e., for each s ∈ S, f(s) is a subset of S. Consider the following
set C: 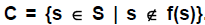If f is a bijection, then there must be some
element c ∈ S such that f(c) = C. Now either c ∈ C or c 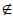C. Prove that in
either case the definition of C leads to a contradiction, so that we conclude
that f could not have been a bijection