NOTE: For the test you must show all work where
appropriate (for instance, solving an equation ). The correct answer
with no proper justification qualifies for NO CREDIT.
Evaluate the piecewise function at the given value of the independent variable.

Determine f(3).

Determine f(3).
Identify the intervals where the function is changing
as requested .
|
3) Increasing |
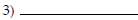 |
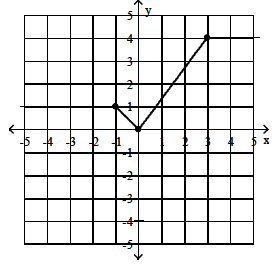
|
4) Constant |
 |
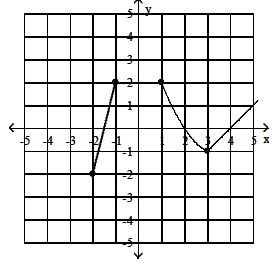
Use the graph of the given function to find any
relative maxima and relative minima.
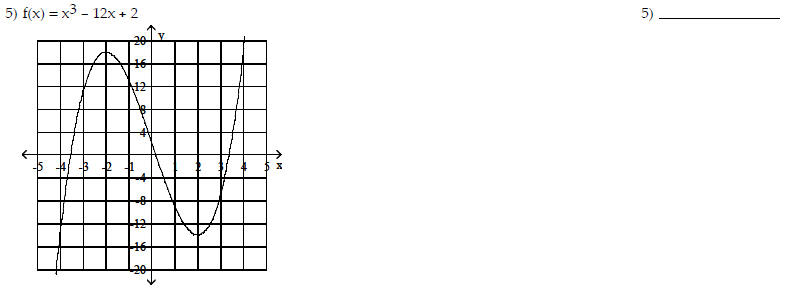
Determine whether the given function is even, odd, or
neither.

Use possible symmetry to determine whether the graph is
the graph of an even function, an odd function, or a function
that is neither even nor odd.

Find the slope of the line that goes through the given
points.

Use the given conditions to write an equation for the
line in point-slope form.
|
11) Passing through (-4, -5) and (-7, -4) |
 |
| |
|
|
12) Passing through (1, -5) with x-intercept = -1 |
 |
Use the given conditions to write an equation for the
line in slope - intercept form .
13) 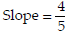 , y-intercept = 5 , y-intercept = 5 |
 |
| |
|
|
14) Passing through (-3, -4) and (-6, -5) |
 |
Graph the line whose equation is given.

Graph the equation in the rectangular coordinate
system .

Determine the slope and the y - intercept of the graph of
the equation.

Graph the linear function by plotting the x - and
y-intercepts.

Use the given conditions to write an equation for the
line in the indicated form.
20) Passing through (3, 2) and parallel to the line whose equation is y
= -2x + 3 ;
point-slope form |

|
| |
|
21) Passing through (3, 4) and parallel to the line whose equation is 3x
+ y - 3 = 0;
slope-intercept form |

|
Find the average rate of change of the function from
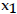 to
to
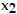 .
.
22) f(x) = -3x2 - x from 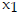 = 5 to = 5 to
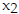 = 6 = 6 |
 |
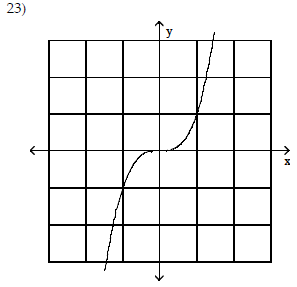
Use the shape of the graph to name the function.
Begin by graphing the standard quadratic function f(x) =
x2 . Then use transformations of this graph to graph the given
function.

Begin by graphing the standard absolute value function
f(x) =l x l. Then use transformations of this graph to graph the
given function.

Find the domain of the function.
