IN CLASS
In the last two lessons we showed how to define matrix multiplication and
division for the solving
of systems of linear equations . In this lesson we define what we call element by
element matrix
operations for applications like the calculation of

for each element in the vector x
INTRODUCTION TO ELEMENT BY ELEMENT CALCULATIONS
1. Multiplication , division and exponentiation
w = [1 2]
x = [3 4]
y1 = w.*x
y2 = w./x
y3 = 1./x
y4 = w.^2
y5 = 2.^w
y6 = w.^x
a. What does .* do
b. What does ./ do
c. What does w.^2 do
d. What does 2.^w do
e. What does w.^x do
f. How do the dimensions of matrices have to be related for element by element
calculations
SOME APPLICATIONS OF ELEMENT BY ELEMENT CALCULATIONS
2. Finding IR in the following circuit with VS = 10 volts for R = 1K, 2K, 3K, 4K
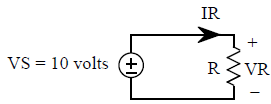
VR = 10;
R = 1000: 1000: 4000;
IR = VR./R
a. Why do we use ./ instead of just / in this program
3. Finding the powers of the resistors in the following circuit
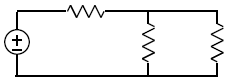
VR = [2 1 0.5];
IR = [1.5e-3 2e-3 1.8e-3];
resistor_powers = VR.*IR
total_resistor_power = sum (resistor_powers)
a. Why do we use .* instead of just * in this program
MORE RESISTOR CIRCUIT EXAMPLES
4. Plotting V2 in the following circuit as a function of R2
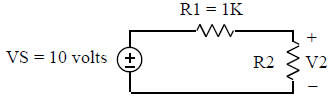
VS = 10;
R1 = 1e3;
R2 = linspace (0, 1e4, 100);
V2 = (R2./(R1 + R2))*VS;
plot (R2, V2)
xlabel ('R2');
ylabel ('V2');
title ('Voltage Division in a Series Circuit');
a. Describe the result of this program
5. Plotting V2 in the following circuit as a function of R1
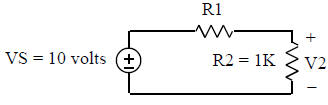
VS = 10;
R2 = 1e3;
R1 = linspace (0, 1e4, 100);
V2 = (R2./(R1 + R2))*VS;
plot (R1, V2)
xlabel ('R1');
ylabel ('V2');
title ('Voltage Division in a Series Circuit');
a. Describe the result of this program
LOG PLOTS
6. First a linear plot
x = linspace (1, 1e5, 200);
y = 1000./(1000 + x.^2);
plot (x, y)
xlabel ('x');
ylabel ('y');
title ('y as a function of x');
a. Describe the result of this program
b. Why did we use ./ rather than /
7. Corresponding log plot
x = linspace (1, 1e5, 200);
y = 1000./(1000 + x.^2);
semilogx (x, y)
xlabel ('x - log scale ');
ylabel ('y - linear scale ');
title ('y on a linear axis and x on a log axis');
a. How did semilogx affect the plot
8. Logspace
w = linspace (0, 2, 5);
y = 10.^w
x = logspace (0, 2, 5)
a. Verify that x = y
b. Make use of the fact that x = y to explain what logspace does
9. Our log plot with logspace
x = logspace (1, 5, 200);
y = 1000./(1000 + x.^2);
semilogx (x, y)
xlabel ('x - log scale');
ylabel ('y - linear scale');
title ('y on a linear axis and x on a log axis');
a. What's the advantage of using logspace for x. What, in particular, is the
advantage of
this program over the one in Problem (7)