1. Find the center and the radius of the circle given by
the equation
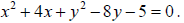
Solution. We will bring the equation to the standard form using
completion of
squares . We complete the squares using the formula
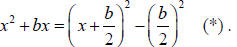 .
.
Let us start with 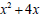 . In this case
. In this case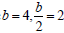 ,
and
,
and 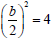 ,
,
whence by formula (*)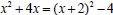 . In a similar way we
. In a similar way we
obtain 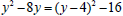 . After we plug in these expressions
into the original
. After we plug in these expressions
into the original
equation we get 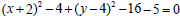 , and finally
, and finally
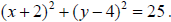
This is the standard equation of a circle with the center at (-2, 4) and the
radius 5.
2. Find the slope- intercept equation of the line perpendicular to the line
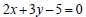
and containing the point (1, 1).
Solution. First we will find the slope of the given line. To do it we
will solve its
equation for y. 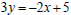 and
and
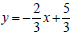 . Therefore the slope of the given line is
. Therefore the slope of the given line is
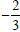 . Because slopes of perpendicular lines are
negative reciprocals the slope of the
. Because slopes of perpendicular lines are
negative reciprocals the slope of the
line we are looking for is 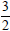 . Next we can
write an equation of this line in the point-
. Next we can
write an equation of this line in the point-
slope form. 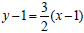 . Finally, solving the last
equation for y we get
. Finally, solving the last
equation for y we get
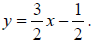
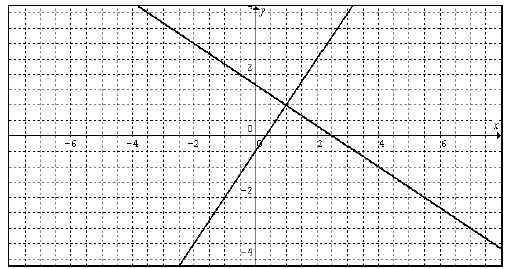
3. Graph both lines from problem 2.
Solution. We can use, for example, the x and y-intercepts of both lines.
For the given line
plugging in y = 0 we find that the x-intercept is at
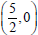 . The y-intercept is at
. The y-intercept is at
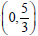 . For
. For
the second line the intercepts are 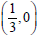 and
and
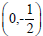 . A computer generated graph is
. A computer generated graph is
shown below.
4. For the quadratic function
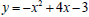 find the coordinates of the vertex , the
find the coordinates of the vertex , the
x- intercepts (if any), and graph the function.
Solution. The coefficients of this quadratic function are
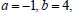 and
and 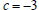 .To
.To
find the coordinates of the vertex we can use the formulas
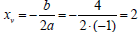 and
and 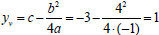 .
Thus the vertex is
.
Thus the vertex is
at (2,1). Because 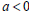 the
vertex will be the highest point of the graph.
the
vertex will be the highest point of the graph.
To find the x-intercepts we have to solve the quadratic equation
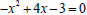 .
.
To do it we can either use the quadratic formula
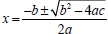 , or in this case
, or in this case
just factor the left part 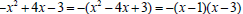 .nyway the x-
.nyway the x-
intercepts are at (1, 0) and (3, 0).
To graph the function we can plot a couple more points in addition to the vertex
and the x-intercepts. It is convenient to notice that for
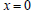 and
and 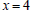 the
function takes
the
function takes
the same value -3.
A computer generated graph is shown below.
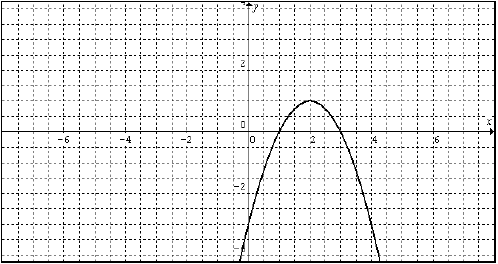
5. A projectile is fired from the ground level with
initial velocity 50 m/sec.
When will it reach the maximum height? What is the maximum height?
Solution. Because we use the metric system a formula for the height of
the projectile at
moment t is 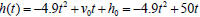 . Thus is a quadratic function of
t
. Thus is a quadratic function of
t
with coefficients 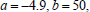 and
and
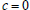 . Because
. Because 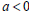 ,
and this quadratic function attains
,
and this quadratic function attains
its greatest value at the vertex. The time when the projectile will reach its
maximum
height equals to the t-coordinate of the vertex,
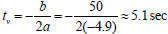 . The
. The
maximum height equals to the h-coordinate of the vertex,
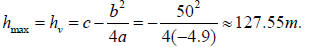
6. A helicopter is 200 m high and moving down with the speed 10m/sec. A
projectile is
fired from the helicopter vertically up with speed 500m/sec.
(a) When will the projectile reach its maximum height?
(b) What is the maximum height?
(c) When it will hit the ground?
(d) What will be the speed of impact?
Solution. We use equations of motion for the metric system.
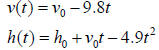
In our case the initial velocity,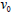 ,
is 500 – 10 = 490 m/sec and the initial height,
,
is 500 – 10 = 490 m/sec and the initial height,
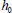 is 200
is 200
m. Thus we have
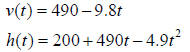
(a) The height of the projectile is a quadratic function of t with
coefficients 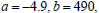 and
and
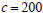 . Because
. Because
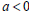 , this quadratic
function attains
, this quadratic
function attains
its greatest value at the vertex. The time when the projectile will reach its
maximum
height equals to the t-coordinate of the vertex,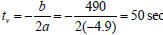 .
.
(b) The maximum height equals to the h-coordinate of the
vertex,
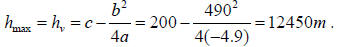 .
.
(c) At the time when the projectile hits the ground its height equals 0.
Therefore we have
to solve the quadratic equation 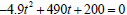 . Applying
the quadratic formula
. Applying
the quadratic formula
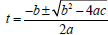 we obtain
we obtain 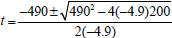 .
Only the positive solution
.
Only the positive solution
makes sense and because the denominator is negative we have to take the negative
sign
in the numerator as well . Therefore the time of impact is
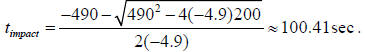
(d) The velocity of impact is 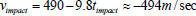 . The speed of
impact is
. The speed of
impact is
the absolute value of the velocity and thus it is approximately
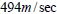 .
.



