Human Age Estimation With Regression on Discriminative Aging Manifold
Abstract—Recently, extensive studies on human faces in the
Human–Computer Interaction (HCI) field reveal significant
potentials
for designing automatic age estimation systems via
face
image analysis. The success of such research may bring in many
innovative HCI tools used for the applications of human-centered
multimedia communication. Due to the temporal property of age
progression, face images with aging features may display some
sequential patterns with low-dimensional distributions. In this
paper, we demonstrate that such aging patterns can be effectively
extracted from a discriminant subspace learning algorithm and
visualized as distinct manifold structures. Through the manifold
method of analysis on face images,the dimensionality redundancy
of the original image space can be significantly reduced with sub -
space learning. A multiple linear regression procedure, especially
with a quadratic model function, can be facilitated by the low
dimensionality to represent the manifold space embodying the
discriminative property. Such a processing has been evaluated
by extensive simulations and compared with the state -of-the-art
methods. Experimental results on a large size aging database
demonstrate the effectiveness and robustness of our proposed
framework.
Index Terms —Age estimation, conformal embedding analysis,
manifold, multiple linear regression, subspace learning.
I. INTRODUCTION
HUMAN-CENTERED COMPUTING (HCC) has long been an extensively
interesting topic in both
Human–Computer Interaction (HCI) and
cognitive studies.The human face, as an information source for HCC,
conveys
significant nonverbal information for the communication and
interaction between humans or between human and machine.
In the vast potential applications of multimedia communication
and HCI, estimating facial attributes, such as human age,
gender, expressions, may often play a crucial role. Particularly,
computer-based automatic human age estimation is receiving
more and more attentions recently [2], [5], [10], [14]. The
applications include security control, image/video retrieval,
and advertisement survey. In particular, age recognition algorithms
can deny young kids access to adult web sites; prevent vending machines
from selling alcohol tounder age people;and
determine the age of people
who spend more time viewing a
particular advertisement.
Apart from a large body of research on aging synthesis and
rendering [1], [10], however, there are relatively few publications
specifically on age estimation. This status is caused by
generally three reasons:1)ageestimation is not a standard classification
problem. Based on different application protocols, it
can be taken as the multiclass classification or regression problems;
2)largesizeagingdatabaseisoftenhardtocollect,espe-
ciallythechronometricalimageseriesforasingleperson;3)as
mentionedin[9],[15],the age progression displayed on facesis
uncontrollable and personalized.Such special characteristics of
aging variation can not be captured accurately due to the prolific
and diversified information conveyed by human faces.
The few existing methods on the age estimation via face images can be
divided into three categories. 1) Anthropometric
model[13].The computation of the sekind of methods is based
on the cranio-facial development theory and facial skin wrinkle
analysis. The growth related changes of face shape and textural
patterns are sufficient to categorize a face into several age
groups. These methods are suitable for the coarse age estimation,
for example, classifying face images into four classes: infant,
teenager, middle-aged people, and the elderly. 2) Aging
pattern subspace [14], [15]. To handle highly incomplete data
due to the difficulty in data collection,AGing pattErn Subspace
(AGES) [14], [15] models a sequence of personal aging face
images by learning a subspace. The age of a test face is deter-
mined by the projection in the subspace that can be strecon struct
the face image.These kind of methods are designed to deal with
the difficulty of utilizing the incomplete age databases. 3) Age
regression[11],[12],[16].In the regression case,facial features
are extracted from an appearance-based shape-texture model.
An input face image is then represented by a set of fitted model
parameters.The regression coefficients are finally estimated ac-
cording to a known regression function. These methods are applicable
to the precise age estimation, since each testing image
will be labelled with a specific age value chosen from a continuous range.
In addition to the foregoing state-of-the-art work, we notice
another essential characteristic of aging factor—the Sequential
Pattern [8]. Since each face image corresponds to a unique age
label, a relatively large size data set should have a significant
trend for some underlying sequential patterns. It is intuitive for
us to apply manifold [17], [18] analysis to age estimation. Un-
fortunately, so far we have not found any literature specifically
pointing out the manifold way of face image analysis for age
estimation. To bring out the advantages of manifold learning,
such methods should be combined with appropriate regression
FU AND HUANG:HUMANAGE ESTIMATION WITHREGRESSION
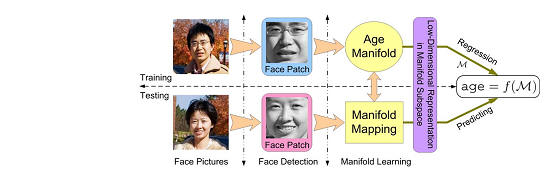
Fig. 1. Framework of age estimation via face image analysis.
models. Moreover, these methods require the size of training
data to be large enough so that it is statistically sufficient to learn
the faithful manifolds.
In this paper, we propose a novel framework of age estimation via multiple
linear regression on the discriminative aging
manifold of face images. The basic idea is to first use the con-
formal embedding analysis to find a sufficient low-dimensional
aging manifold subspace that embodies the discriminative property.
Then we model the manifold representation with a multiple
linear regression procedure based on a quadratic function. For
a new testing image, we fit the extracted low-dimensional feature with
the learned regression model to estimate the exact age
or an age interval. Extensive experiments on our large size internal
data base demonstrate the effectiveness and robustness of
our proposed framework compared with several state-of-the-art
methods.
In the rest of the paper, we first introduce the details of our
proposed age estimation framework in Section II. The experimental
result sand discussions are then presented in Section III.
We conclude the paper and provide some future directions in the
last section.
II. AGING MANIFOLD LEARNING AND REGRESSION
Since the high dimensionality of the original training image
may often lead to the failure of regressors,an appropriate manifold
learning algorithm is required to first reduce the dimension-
ality redundancy.In this paper,such a manifold embedding formulation
is defined to embody a subspace learning procedure.
A. Framework of Human Age Estimation
Our age estimation framework mainly integrates three modules:
face detection, discriminative manifold learning, and
multiple linear regression. Fig. 1 illustrates the diagram of the
framework. In the training stage, we collect face images from
a broad range of subject ages. An automatic face detector [25]
is used to detect and crop the face image patches from all the
training images. Some standard alignments are then performed
to normalize the training features, such as scaling the image
size according to the locations of canthus. The discriminative
aging manifold is learned to map the original data into a
low-dimensional subspace that is sufficiently discriminative.
We then use a multiple linear regression procedure with a
quadratic function to estimate a statistical age model over the
low-dimensional representation. In the testing stage, an input
face image is transformed to the low-dimensional aging feature
in the same way. The age label is predicted through fitting the
regression model on the learned manifold representation.
B. Discriminative Aging Manifold Learning
Suppose the image space is represented by a set of aligned face images
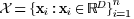 of subjects in the order of subjects' ages. A
ground of subjects in the order of subjects' ages. A
ground
truth set
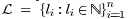 associated with the images provides the age associated with the images provides the age
label. Our goal
is to learn a low-dimensional discriminative manifold embedded
in as well as
a low-dimensional representation y=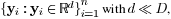
which is a
one-to-one
mapping
to X.More specifically,the projection from the
image space to
the manifold space can be modelled as (1):
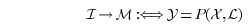
where P(•) denotes the projection function, which can be either
linear or
nonlinear.
Considering the label information in
this modeling, we adopt
a supervised learning
approach to find P(•) Due to the limited generalization
capability of nonlinear
methods in
the test cases of real-world applications
[19], we
adopt a linear strategy in this paper
to learn the manifold embedding.
Since the final age estimation comes down to classification,
we want to learn a manifold embedding that is sufficiently discriminative [3],
[24], [29].
Hence, based on the graph embedding theory[23],we define two -node graphs,
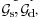 and
their
corresponding and
their
corresponding  affinity matrices, affinity matrices, The
i-th node of the graph The
i-th node of the graph
represents the
data point
xi For the graph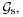 we only consider each
pair of we only consider each
pair of
data xi and xj from the same
class with 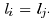 For the graph For the graph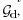 we
only consider we
only consider
each pair of data xi and xj from the
different
class with
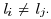 An edge is constructed An edge is constructed
between nodes i and
j if xj is among the
ks or kd nearest neighbors of
xi
and vice
versa, where parameters ks and kd are
chosen
empirically. If node i and j are
connected,
the weight of the edge between xi and xj is set by
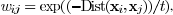 where t where t
is a free parameter to be tuned empirically.Otherwise,wij=0
if node i and j are not
connected.Following our previous work of Conformal Embedding
Analysis(CEA)[3]
on
face images,the
Dist(xi,xj) is defined by a linear function of the
centered
Pearson correlation coefficient[30] between
xi and xj that is Dist(xi,xj)=1-ρi,j. we have
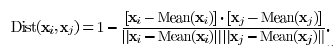
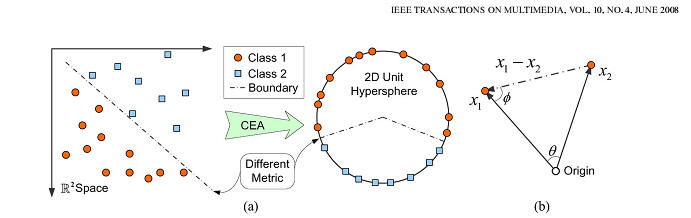
Fig. 2. Geometric interpretation of CEA. (a) CEA perspective with the data
normalization. (b)
Correlation measure of the objective function.
In a geometric sense, the correlation metric projects the
original data points onto a high-dimensional unit hypersphere
with data centering and normalization. Fig. 2(a) illustrates
the CEA perspective on a toy data set. Note that the distance
metric is changed from the Euclidean to cosine-angle. Such
a measurement provides the image feature extraction with a
tolerance against gray-level variations, which has been amply
demonstrated by [27], [29] and [3].
Directly measuring the correlation between two data vectors
leads to iteratively solving a nonconvex objective function[30].
For simplicity, we want to find an approximate measure which
can lead to a closed-form solution. Consider the simplest case
of a pair of data points x1 and x2 in Fig.2(b). Intuitively, meauring θ
is highly related to simultaneously measuring 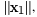 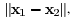
and 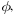 because the length values of the two
adjacent sides because the length values of the two
adjacent sides
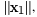 and and 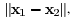 and the
included angle, and the
included angle,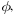 ,can exactly determine the ,can exactly determine the
triangle constructed by x1,x2,and θ.Therefore, following our previous
work in [3], CEA objective function is defined as follows:
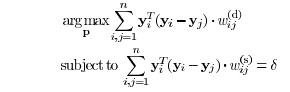
where δ is a constant number, such as 1. The weight matrices
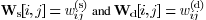 are symmetric and nonnegative are symmetric and nonnegative
They are defined over all data points to model the local
correlational affinity structure of the manifold.The basic criteria
for setting the weights is to penalize the distance measure between
each two data points via the pairwise weight to infer the
embedding.The above objective function achieves the discriminative
learning by preserving the pairwise correlation metric
between the data points in the same class,while minimizing the
pair wise correlation metric between the data points from the different
classes at the same time.
Define the 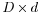 projection matrix projection matrix 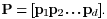 The basic idea for
The basic idea for
learning the
manifold space is to find the matrix P satisfying
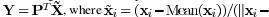
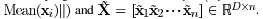 Following
the matrix formulation Following
the matrix formulation
in [3], (3) can
be
rewritten as
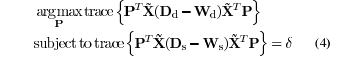
where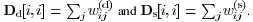 Equation Equation
(4) can be solved in a closed form through the following reformulation,
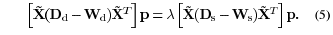
The column vectors 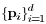 of the
projection matrix indicate the eigenvectors of of the
projection matrix indicate the eigenvectors of
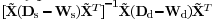 corresponding to the large steigen
values,which corresponding to the large steigen
values,which
can be solved
by SVD.
The above CEA manifold learning algorithm has the following properties:
1) this is a supervised subspace learning
method, which is provided with boosted discriminative power
by incorporating the labeling in formation of both neighborhood
and class to each sub-manifold. Such a strategy conforms to
the Fisher Criterion [7] so as to be more reliable for the multiclass
classification problems; 2) since the high-dimensional
data are modeled and embedded with a local affinity graph
in the correlational mapping manner, the learned manifold
embodies a different geometric intuition from related methods,
such as LDA [28], LDE [24], or MFA [23]; 3) the CEA also
differentiates itself from CDA [30] with a different objective
function and a different solution;4)the learned image subspace
is gray-level variation tolerant [3] since the correlation metric
enhances the robustness of the feature extraction [30]. 5) the
CEA performance is not sensitive to the two parameters
and , when they are relatively large. The parameter may
distinctly influence the CEA performance.But,acommon constant,
without too much tuning, is good enough for reasonable
CEA classification.
C. Regression on Discriminative Aging Manifold
After finding the low-dimensional representation of the original
image space via manifold embedding,we define the agees-
timation as a multiple linear regression problem[6] in the manifold space.
Equation (6) specifically describes this regression
model,
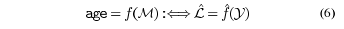
where 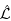 denotes the estimated age label,ƒ(•)
the unknown regression function, denotes the estimated age label,ƒ(•)
the unknown regression function,
and ƒ(•) the estimated regression function.In
a matrix formulation, we have
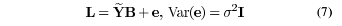
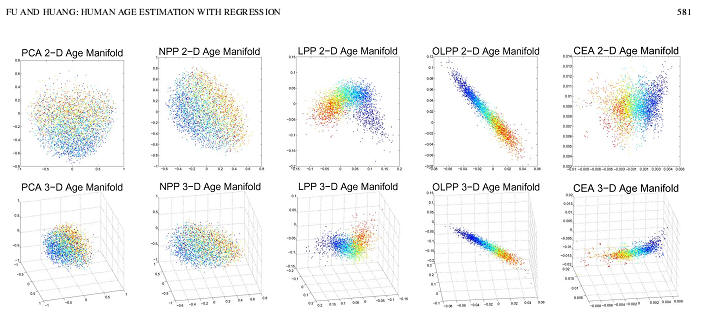
Fig.3.
The2-Dand3-D aging manifold visualization using PCA,NPP,LPP,OLPP,and CEA algorithms
respectively.The color of the points representsage with
blue being the youngest and red the
oldest.
where L is the age label vector. 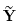 is a known matrix including is a known matrix including
a column of 1 for the intercept and all the observed values for
the rest. The vector B is the unknown parameter vector which
we need to estimate during the learning stage. The error vector
consists of unobservable random variables, assumed to have
zero mean and be uncorrelated, with common variance σ2.To
fit the model,B is estimated by Ordinary Least Squares (OLS)
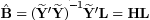 or robust regression, and the fitted or robust regression, and the fitted
value of is then given by

The vector of residuals is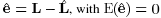 and and
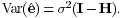 Suggested by the previous work in [11], Suggested by the previous work in [11],
[12],we adopt a quadratic function for the regression.Taking the
corresponding low-dimensional representation of each image in
the manifold space as the aging feature,(9) formulates the fitted
age estimation model. For each of yi of xi
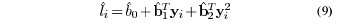
where 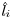 denotes the estimated age for the image
xi, denotes the estimated age for the image
xi,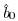 the estimated the estimated
intercept term,
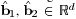 the estimated parameter vectors, and the
yi2 the estimated parameter vectors, and the
yi2
arraywise square of y i.Hence, we have
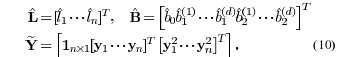
Compared with the quadratic function for regression in such
a scenario, the linear function may lead to an under-fitting of
the result; and the cubic or higher order function may over-fit
the data. The evidences to support this conclusion are provided
by the experiments in the next section.
III. EXPERIMENTS
As we mentioned in the beginning, data collection is crucial
for the precise age estimation. However, it is extremely hard in
practice to collect a large size aging database, especially when
one want to collect the chronometric image series from an indi-
vidual. In addition to the novel age estimation framework, this
paper also introduces a new real-world aging data base collected
in our project, which satisfies the particular experimental pro-
tocol for estimating precise human ages through face images.
A. Data Collection
The age estimation performance is tested on our UIUC-IFP
internal aging database.1 The database contains 8000 high-res-
olution RGB color face images in total. Specifically, there are
1600 different voluntary Asian subjects, 800 female and 800
male, with ages ranging from 0 to 93 years (we have newborn
subjects).Each subject has about five near frontal images and a
ground truth label of his or her approximate age as an integer.
Since the photo graphs are taken in an outdoor environment with
spontaneous subject attentions, the data have significant vari-
ances on illumination,facial expression,and makeup.In the ex-
periments,we first run a face detector introduced in [25] to find
the face area in each image; and then label the eye corner loca-
tions of each subject. The face images are finally cropped, re-
sized,and transformed to 60×60 gray-level patches according
to the detection and labeling results. After reshaping the image
matrices to vectors, each datum has a dimension of 3600.
B. Aging Manifold Visualization
To observe the aging manifolds,we choose the 4000 face images
of female subjects to visualize the embedded low-dimensional
manifold.Fig.3 displays the2-D and 3-D manifold visualizations
of the PCA[26],NPP[22],LPP[19],OLPP[21],and
CEA[3] algorithms respectively.Each data point represents one
faceimage.The data point sofagefrom0to93arecoloredfrom
blue to red. We choose four nearest neighbors for all the graph
embedded learning algorithms. We can see that, since PCA is
un-supervised, it produces a mapping with no clear manifold
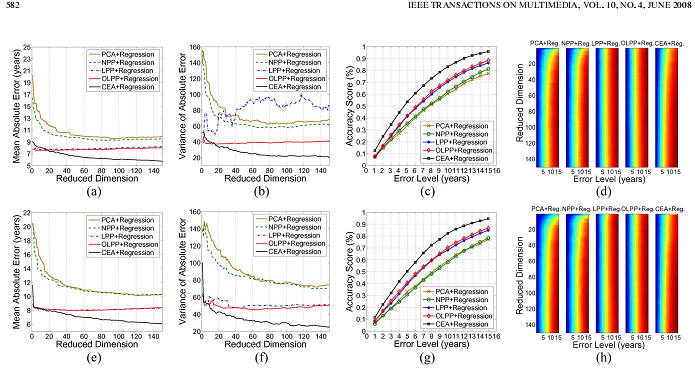
Fig.4. Age estimation results on the UIUC-IFP internal aging database
using PCA+regression,NPP+regression,LPP+regression,OLPP+regression,andCEA+re-
gression algorithms.(a)–(d)are for the female subjects,and(e)–(h)forthemalesubjects.(a),
(e)MA
Eversus dimensionality.(b),(f)Variance versus dimensionality.(c), (g) Accuracy score
versus error level. (d), (h) Accuracy score versus error
level and dimensionality.
Red implies better performance.
trend or structure. NPP does not yield obvious improvement
over PCA. Compared with PCA and NPP, both LPP and OLPP
achieve much better visualization results with distinct manifold
trend and structure in a chronological series.LPP forms the ap-
proximate manifold into a curve, while OLPP forms a straight
line. The manifold formed by CEA is in a dispersal type and
following a curved chronological trend. We can see that LPP,
OLPP,and CEA all reveal clear clusters and discriminative pat-
terns in the visualization.
C. Age Estimation
We choose to separate the UIUC-IFP database into two sub-
sets, 4000 female and 4000 male images, and experiment on
them separately.The reason for separating the two subsets is that
the correlation between ground truth age and the corresponding
appearance age is different for males and females. The appear-
ance age of female is more apt to be altered by make-ups and
accessories than the appearance age of male. For each of the
two cases,we randomly select 2000 images for training and the
rest 2000 images for testing. Following our previous work in
[2],we choose 150 as the upper limit for the dimension of each
learned manifold subspace. Note that the original image space
has a dimension of 3600. Fig. 4 summarizes and compares the
results of the PCA+regression, NPP+regression, LPP+regres-
sion,OLPP+regression,and CEA+regression algorithms for the
twocasesrespectively.Fig.4(a)–(d) are for the female subjects,
and (e)–(h) for the male subjects. (a) and (e) show the Mean
Absolute Error(MAE) of the absolute error against the reduced
dimension number. (b) and (f) show the variance of the abso-
lute error against the reduced dimension number. We observe
that both LPP+regression and OLPP+regression achieve com-
parable results with about eight years of MAE, and outperform
the PCA+regression and NPP+regression in both of the eval-
uations. OLPP+regression has a stable and lower variance in
the estimation than that of the LPP+regression.CEA+regression
performs the best for both male and female subjects with about
five to six years of MAE. The improvement is statistically sig-
nificant.From the consistent decline of the curvesgenerated by
CEA+regression, we see a large potential for further improve-
ment if we increase the upper limit for the number of dimensions
of the learned manifold subspace. Another interesting observa-
tion is that the overall estimation result for the males is consis-
tently different from the females in each kind of evaluation.This
justifies the decision we made to separate the two cases for the
respective evaluations.
Fig. 4(c) and (g) show the accuracy score of the five algo-
rithms against the estimation error levels (age error tolerance)
from one to 15 years. It can be seen that the LPP+regression
and OLPP+regression are still comparable and significantly out-
perform the PCA+regressionand NPP+regression.This is con-
sistent with the manifold visualization results.CEA+regression
still significantly improves all the other methods consistently on
all the error levels.(d)and(h) plot the accuracy score against the
error levels and the reduced dimensionality. The red and blue
color indicate large and small value of the accuracy scores re-
spectively. Compared with the PCA+regression and NPP+re-
gression, LPP+regression, OLPP+regression and CEA+regres-
sion have more stably distributed discriminative power against
both error level and dimension changes.This phenomenon guar-
antees the robustness of the algorithms.
D. Discussion
From the above evaluations, we can see that PCA and NPP
perform the worst in both manifold visualization and age es-
timation for all the dimensionality reduction cases. LPP and
 Fig. 5. Age estimation comparisons on the linear, quadratic, and cubic
regression functions
for female face images using CEA+regression. (a) MAE versus
dimensionality. (b) Variance
versus dimensionality. (c) Accuracy score versus
error level. (d) Accuracy score versus error
level and subspace dimensionality using
CEA+quadratic regression.
OLPP achieve superior performance in both manifold visual-
ization and age estimation in very low-dimensional subspaces,
such as twoor three dimensions.CEA shows its superiority for
most of the dimensionality reduction cases,especially when the
subspace dimensionality is a little higher.The seresults indicate
that the human aging manifold is not sufficiently represented by
such a low number of dimensions. Obviously, there are person,
gender, illumination, and occlusion variations in the face im-
ages. The visualization of CEA manifold shows not only the
main trend of the aging manifold like OLPP ,but also some local
sub-trends that describe the other incidental variations. This is
one possible reason to explain why CEA+regression outper-
forms the other methods in the comparison forage estimation.
To demonstrate the effectiveness of the regression using a
quadratic function,we compare its age estimation performance
with the regression using the linear or cubic function for the fe-
male face images. Fig. 5(a)–(c) show the experimental results
yielded by CEA+regression.(a) and (b) show the MAE and the
variance of the absolute error against the reduced dimensions for
the three regression cases. (c) shows the accuracy score of the
three regressions against the estimation error levels from one
to 15 years. It is obvious that CEA+quadratic regression con-
sistently outperforms CEA+linear regression and CEA+cubic
regression with significant improvements.These overall results
are consistent with the reports from [11], [12]. We can see that
the cubic regression has an over-fitting while the linear regres-
sion has an under-fitting compared with the quadratic regression
in such a specific scenario. (d) shows the accuracy score of the
three regressions against the estimation error level and subspace
dimensionality (50, 100, 300, 700, 800) using CEA+quadratic
regression.We observe that a subspace dimensionality of about
300 yields the best performance. This observation can provide
an empirical guidance for choosing the size of the manifold
space.
IV. CONCLUSIONS
We have proposed a novel pattern classification framework
for estimating human age through quadratic regression on the
discriminative aging manifolds.The extensive experimental re-
sults demonstrate that CEA can extract effective aging features
for both manifold visualization and pattern discriminating in the
regression ways of age estimation. Regression using quadratic
functions is better than using linear or cubic functions which
may encounter under-fitting or over-fitting in the aging manifold
space. In the future work, we will develop a new age estimation
framework based on support vector machine classification
or support vector regression techniques and compare it with the
proposed one.We are also interested in using tens or analysis [4]
to extract aging features for a possible extension of our system
framework.
REFERENCES
[1] Y. Fu and N. Zheng, “M-face: An appearance-based photorealistic
model for multiple facial attributes rendering,” IEEE Trans. Circuits
Syst. Video Technol., vol. 16, no. 7, pp. 830–842, 2006.
[2] Y. Fu, Y. Xu, and T. S. Huang, “Estimating human age by manifold
analysis of face pictures and regression on aging features,” in IEEE
Conf. ICME’07, 2007, pp. 1383–1386.
[3] Y. Fu, M. Liu, and T. S. Huang, “Conformal embedding analysis
with local graph modeling on the unit hypersphere,” in IEEE Conf.
CVPR’07, Workshop on Component Analysis, 2007.
[4] Y. Fu and T. S. Huang, “Image classification using correlation tensor
analysis,” IEEE Trans. Image Process., vol. 17, no. 2, pp. 226–234,
Feb. 2008.
[5] G.Guo,Y.Fu,T.S.Huang,andC.Dyer,“Locally adjusted robust re-
gression for human ageestimation,”in IEEE Workshop on Applications
of Computer Vision, 2008.
[6] S.Weisberg,Applied Linear Regression,3rded. Hoboken,NJ:Wiley
Interscience, 2004.
[7] R. O. Duda, E. H. Peter, and G. S. David, Pattern Classification, 2nd
ed. Hoboken, NJ: Wiley Interscience, 2000.
[8] K.A.Deffenbacher,T.Vetter,J.Johanson,andO’Toole,“Facialaging,
attractiveness,and aistinctiveness,”Perception,vol.27,pp.1233–1243,
1998.
[9] N. Ramanathan and R. Chellappa, “Face verification across age pro-
gression,”IEEETrans.ImageProcess.,vol.15,no.11,pp.3349–3361,
2006.
[10] N.Ramanathan and R.Chellappa,“Modeling age progression in young
faces,” in IEEE Conf. on CVPR’06, 2006, pp. 387–394.
[11] A. Lanitis, C. Taylor, and T. Cootes, “Toward automatic simulation
of aging effects on face images,” IEEE Trans. Pattern Anal. Machine
Intell., vol. 24, no. 4, pp. 442–455, 2002.
[12] A.Lanitis,C.Draganova,and C.Christodoulou,“Comparing different
classifiers for automatic age estimation,” IEEE Trans. Syst, Man, Cy-
bern. B., vol. 34, no. 1, pp. 621–628, Feb. 2004.
[13] Y. H. Kwon and N. da Vitoria Lobo, “Age classification from facial
images,” Computer Vis. Image Understand., vol. 74, no. 1, pp. 1–21,
1999.
[14] X. Geng, Z.-H. Zhou, Y. Zhang, G. Li, and H. Dai, “Learning from
facial aging patterns for automatic age estimation,”in ACM Conf.Mul-
timedia (ACM MM’06), 2006, pp. 307–316.
[15] X.Geng,Z.-H.Zhou,and S.-M.Kate,“Automatic age estimation based
on facial aging patterns,” IEEE Trans. Pattern Anal. Machine Intell.,
vol. 29, no. 12, pp. 2234–2240, 2007.
[16] S.Yan,H.Wang,T.S.Huang,Q.Yang,and X.O.Tang,“Ranking with
uncertain labels,” in IEEE Conf. ICME’07, 2007.
[17] H. S. Seung and D. D. Lee, “The manifold ways of perception,” Sci-
ence, vol. 290, no. 5500, pp. 2268–2269, 2000.
[18] S. T. Roweis and L. K. Saul, “Nonlinear dimensionality reduction by
locally linear embedding,”Science,vol.290,no.5500,pp.2323–2326,
2000.
[19] X. He and P. Niyogi, “Locality preserving projections,” in Proc.
NIPS’03, 2003.
[20] X. He, S. Yan, Y. Hu, P. Niyogi, and H.-J. Zhang, “Face recognition
using laplacianfaces,” IEEE Trans. Pattern Anal. Machine Intell., vol.
27, no. 3, pp. 328–340, 2005.
[21] D.Cai,X.He,J.W.Han,andH.-J.Zhang,“Orthogonal laplacianfaces
for face recognition,”IEEE Trans.Image Process.,vol.15,no.11,pp.
3608–3614, Nov. 2006.
[22] Y. W. Pang, L. Zhang, Z. K. Liu, N. H. Yu, and H. Q. Li, “Neigh-
borhood Preserving Projections (NPP): A novel linear dimension re-
duction method,” in Int. Conf. on Intelligent Computing, 2005, pp.
117–125.
[23] S. Yan, D. Xu, B. Zhang, H. Zhang, Q. Yang, and S. Lin, “Graph em-
bedding and extension:Ageneral framework for dimensionality reduc-
tion,” IEEE Trans. Pattern Anal. Machine Intell., vol. 29, no. 1, pp.
40–51, Jan. 2007.
[24] H.-T. Chen, H.-W.Chang, andT.-L.Liu, “Local discriminant embed-
ding and its variants,” in IEEE Conf. CVPR’05, 2005,pp. 846–853.
[25] P. Viola and M. Jones, “Robust real-time object detection,” Int. J.
Comput. Vis., vol. 57, no. 2, pp. 137–154, 2004.
[26] M.A.TurkandA.P.Pentland,“Face recognition using eigenfaces,”in
IEEE Conf. CVPR’91, 1991, pp. 586–591.
[27] B.V.K.Vijaya Kumar,R.D.Juday,and A.Mahalanobis,Correlation
Pattern Recognition. : Cambridge Univ. Press, 2006.
[28] P. N. Belhumeur, J. P. Hepanha, and D. J. Kriegman, “Eigenfaces vs.
Fisherfaces: Recognition using class specific linear projection,” IEEE
Trans. Pattern Anal. Machine Intell., vol. 19, no. 7, pp. 711–720, Jul.
1997.
[29] T.-K. Kim, J. Kittler, and R. Cippola, “Discriminative learning and
recognition of image set classes using canonical correlations,” IEEE
Trans. Pattern Anal. Machine Intell., vol. 29, no. 6, pp. 1005–1018,
Jun. 2007.
[30] Y.Ma,S.Lao,E.Takikawa,andM.Kawade,“Discriminant analysis in
correlation similarity measure space,”in Int.Conf.Machine Learning,
2007, pp. 577–584.
 |
Yun Fu (S’07) received the B.E. degree in informa-
tion engineering from the School of Electronic and
Information Engineering, Xi’an Jiaotong University,
China, in 2001, the M.S. degree in pattern recogni-
tion and intelligence systems from the Institute of
Artificial Intelligence and Robotics, Xi’an Jiaotong
University, in 2004, and the M.S. degree in statis-
tics from the Department of Statistics, University
of Illinois at Urbana-Champaign, in 2007. He is
currently pursuing the Ph.D. degree in the Electrical
and Computer Engineering Department, University of
Illinois at
Urbana-Champaign. |
His research interests include human computer interaction,machine learning,
image processing, multimedia and computer vision.
Mr. Fu is the recipient of a 2002 Rockwell Automation Master of Science
Award, two Edison Cups of 2002 GE Fund “Edison Cup” Technology Inno-
vation Competition, 2003 HP Silver Medal and Science Scholarship for Excel-
lent Chinese Student,2007 Beckman Graduate Fellowship,2007 DoCoMo USA
Labs Innovative Paper Award (IEEE ICIP’07 best paper award), 2007 Chinese
Government Award for Outstanding Self-financed Students Abroad, and 2008
M.E.VanValkenburg Graduate Research Award.He is a student member of In-
stitute of Mathematical Statistics (IMS), and a 2007–2008 Beckman Graduate
Fellow.
 |
Thomas S.Huang(S’61-M’63-SM’76-F’79-LF’01)
received the B.S. degree in electrical engineering
from National Taiwan University, Taipei, Taiwan,
R.O.C., and the M.S. and Sc.D. degrees in electrical
engineering from the Massachusetts Institute of
Technology (MIT), Cambridge.
He was at the faculty of the Department of Elec-
trical Engineering at MIT from 1963 to 1973, and at
the faculty of the School of Electrical Engineering
and Director of its Laboratory for Information
and Signal Processing at Purdue University, West |
Lafayette, IN, from 1973 to 1980. In 1980, he joined the University of
Illinois
at Urbana-Champaign, where he is now William L. Everitt Distinguished
Professor of Electrical and Computer Engineering, Research Professor at the
Coordinated Science Laboratory, Head of the Image Formation and Processing
Group at the Beckman Institute for Advanced Science and Technology, and
Co-chair of the Institute’s major research theme: human-computer intelligent
interaction. His professional interests lie in the broad area of information
technology, especially the transmission and processing of multidimensional
signals. He has published 20 books and over 500 papers in network theory,
digital filtering, image processing, and computer vision.
Dr. Huang is a Member of the National Academy of Engineering, a Foreign
Member of the Chinese Academies of Engineering and Science, and a Fellow
of the International Association of Pattern Recognition, IEEE, and the Optical
Society of America, and has received a Guggenheim Fellowship, an A. von
Humboldt Foundation Senior US Scientist Award, and a Fellowship from the
Japan Association for the Promotion of Science. He received the IEEE Signal
Processing Society’s Technical Achievement Award in 1987, and the Society
Award in 1991. He was awarded the IEEE Third Millennium Medal in 2000.
Alsoin 2000,he received the Honda Lifetime Achievement Award for “contri-
butions to motion analysis.”In 2001,he received the IEEE JackS.Kilby Medal.
In 2002, he received the King-Sun Fu Prize, International Association of Pat-
tern Recognition, and the Pan Wen-Yuan Outstanding Research Award.He is a
Founding Editor of the International Journal of Computer Vision,Graphics,and
Image Processing and Editor of the Springer Series in Information Sciences.
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
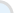 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
February 12th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
Step 2 :
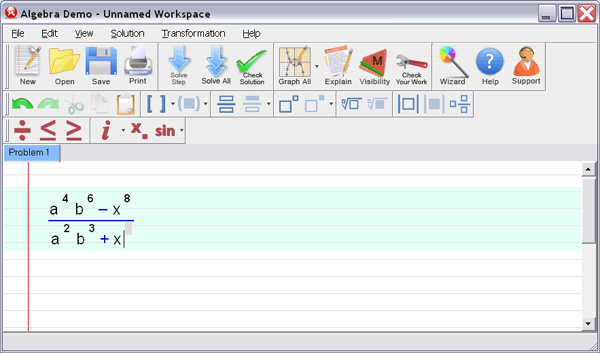
Let Algebra Helper solve it:
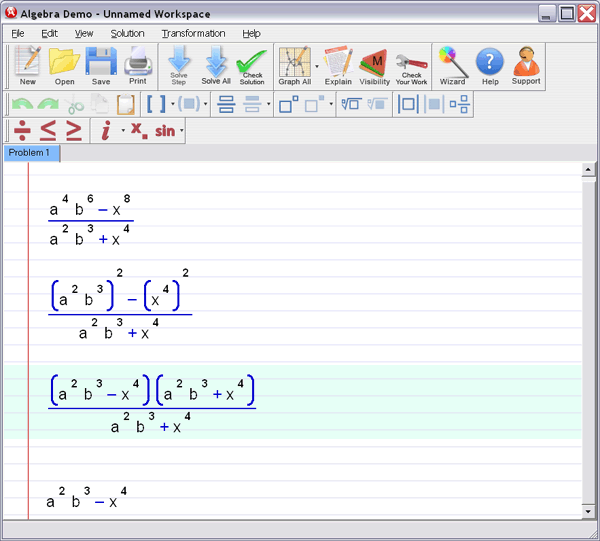
Step 3 : Ask for an explanation for the steps you don't understand:
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



