1. Inequalities
-An inequality is a comparison of two values.
-There are three possible relationships between two different values.
Greater than, less than, or equal to.
-Four symbols are used to represent these relationships (<,>,≤, ≥).
Example: 3<5
In this case the inequality states that 3 is less than 5.
-Think about the symbol as an arrow that always points toward the smaller value.
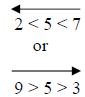
-Inequalities also work with variables.
Example: x<5 means that x can be any value that is
less than 5.
Example: 3≤x means that x is any number greater
than or equal to 3.
2. Graphing Inequalities in One Variable
-Inequalities in one variable can be graphed on a number
line .
Example: x<5 would be graphed as

If x is less than or greater than, you should use a
parenthesis or an open
circle because 5 is not included in the set.
Example: 3≤x would be graphed as

In this case a bracket or a closed circle is used because
3 is included in the
set.
Examples: x>9
12<x
3≤x<5
3. Interval Notation
Another method of representing inequalities is with
interval notation.
Example: 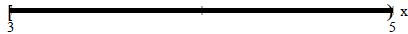
This can be written as 3≤x<5 or [3,5)
which is known as Interval Notation
-From this notation you can see that there is a left
boundary and a right boundary.
In this case the left boundary is at 3 and the right boundary is at 5.
-When you have a parenthesis or a greater than or less
than symbol the number is
not included in the set, but that does not mean that you cannot include numbers
close to it.
By this we mean numbers such as 4.1, 4.5, 4.9, and 4.999.
-What happens if one of the boundaries is removed?
Example: x<5
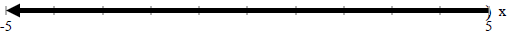
In this case the values of x go on forever in the negative
direction.
We can represent this inequality in interval notation as (-∞,5), where the
infinity symbol (∞) is used to represent that there is no endpoint for the
values of x.
Examples: x ≥3
x<15
3<x<15
4. Solving Linear Inequalities
- Linear inequalities involve one variable.
x+3<4 is a linear inequality.
-All of the rules that apply to equations also apply to
inequalities with one
important exception.
If you ever multiply or divide by a negative number you
must reverse
the direction of the inequality sign .
Example: 4x-6 > 2x+10
Add 6 to both sides: 4x-6+6 > 2x+10+6
Subtract 2x from both sides: 4x-2x > 2x+16-2x
Divide both sides by 2: 2x/2 > 16/2
Answer: x>8 or (8,∞)
Example: x+3 > 4x+6
Subtract 3 from both sides: x+3-3 > 4x+6-3
Subtract 4x from both sides: x-4x > 4x+3-4x
Divide both sides by -3: -3x/-3 > 3/-3
Change the direction of the inequality.
Answer: x<-1 or (-∞,-1)
Example: 5(x-2) ≥ 9x-3(2x-4)
-When you solve an inequality the solutions can be written
in interval notation or
set builder notation.
Set builder notation:
{x|x≤5} and {x|5<x≤9}
This notation says that x is any value that satisfies the
inequality in the notation.
5. Solving Compound Inequalities
-Compound inequalities involve two inequalities of the
same variable.
Example: -3<2x+1<5
can be written as two inequalities
-3<2x+1 and 2x+1<5
Each inequality is solved separately.
Another method is to apply properties of equations to all
parts of the
inequalities.
Example: -3 < 2x+1 < 5
Can be solved as follows:
Subtract 1 from all parts: -3-1 < 2x+1-1 <5-1
Divide all parts by 2: -4/2 < 2x/2 <4/2
Answer: -2 < x < 2 or (-2,2) or {x|-2<x<2}
6. Solving Absolute Value Inequalities
-Solving inequalities involving absolute values requires
learning 2 new rules that
will affect how the problem is solved.
A. When solving an inequality in which the absolute value
expression is less than
(<) or less than or equal to (≤) a standard expression, such as |x+3| ≤ 5, we
must
rewrite this as -5≤x+3≤5 and solve.
B. When solving an inequality in which the absolute value
expression is greater
than (>) or greater than or equal to (≥) a standard expression, such as
|2x-1|>7, we
must rewrite this as 2x-1<-7 or 2x-1>7 and solve each inequality separately.
Example: |x+3|≤5
Rewrite: -5≤x+3≤5
Subtract 3 from all parts: -5-3≤x+3-3≤5-3
Simplify : -8≤x≤2 or [-8,2] or {x|-8≤x≤2}
Example: |2x-1|>7
Rewrite: 2x-1<-7 or 2x-1>7
Add 1 to both sides of each inequality: 2x-1+1<-7+1 or 2x-1+1>7+1
Divide both sides of each inequality by 2: 2x/2<-6/2 or 2x/2>8/2
Simplify: x<-3 or x>4 , (-∞,-3) ∪ (4,∞), or {x| x<-3 or x>4}
Example: |-2x+5|<1



