Fields and rings
To understand IDEA, AES, and some other modern
cryptosystems, it is necessary to
understand a bit about finite fields.
A field is an algebraic object . The elements of a field can be added and
subtracted and
multiplied and divided (except by 0). Often in undergraduate mathematics courses
(e.g.,
calculus and linear algebra ) the numbers that are used come from a field. The
rational
numbers: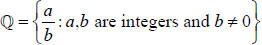
form a field; fractions can be added
(and
subtracted) and multiplied (and divided). The real numbers form a field. The
complex numbers form a field. RC
Number theory studies the integers Z. The integers do not form a field. Integers
can be
added (and subtracted) and multiplied, but integers cannot always be divided.
Sure, 6
divided by 3 is 2; but 5 divided by 2 is not an integer;
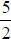is a rational number . The
integers form a ring, but the rational numbers form a field.
Similarly the polynomials with integer coefficients form a ring. We can add (and
subtract) polynomials with integer coefficients, and the result will be a
polynomial with
integer coefficients. We can multiply polynomials with integer coefficients, and
the
result will be a polynomial with integer coefficients. But, we cannot always
divide
polynomials with integer coefficients: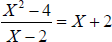 
, but
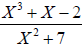is not a
polynomial – it is a rational function. The polynomials with integer
coefficients do not
form a field, they form a ring. The rational functions with integer coefficients
form a
field.
A field has two operations ; they are usually written as addition and
multiplication.
Subtraction is just the inverse of addition; it is adding the additive inverse
(e.g., 5 – 4 = 5 + (-4) = 1). Division is just the inverse of multiplication; it
is multiplying
by the multiplicative inverse (e.g.,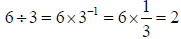 
). A
ring also has two
operations – addition and multiplication – and, although addition is assumed to
have an
inverse, in a ring it is not assumed that multiplication has an inverse.
( Addition and
multiplication are also assumed to have several other properties . For both a
ring and a
field, it is assumed that addition commutes and is associative. For both a ring
and a field,
it is assumed that multiplication distributes over addition. For a field but not
for a ring,
multiplication is assumed to be commutative.)
The fields that we commonly used in mathematics courses (, , and C) are
infinite.
For cryptological purposes, finite fields are useful.
Finite field of p elements
Recall that the integers mod 26 do not form a field. The integers modulo 26 can
be added
and subtracted, and they can be multiplied (so they do form a ring). But, recall
that only
1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, and 25 have multiplicative inverses mod
26; these are
the only numbers by which we can divide. These twelve numbers are the positive
integers that are less than or equal to 26 and relatively prime to 26.
Recall that given an integer that is less than or equal to n and relatively
prime to n we
can use the extended Euclidean algorithm to find its inverse mod n. So, it is
possible to
construct the multiplicative inverses of 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23,
and 25 modulo
26. If the modulus is prime, we can construct an inverse for each positive
integer that is
less than or equal to the modulus.. So, for each prime p we can construct a
finite field of
p elements – the integers mod p.
The integers mod 5 is a field of 5 elements {0, 1, 2, 3, 4}. Here are the
addition and
multiplication tables:
|
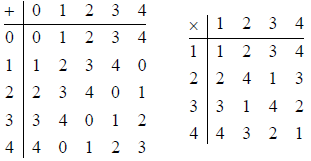
number |
additive |
number |
multiplicative inverse |
 |
|
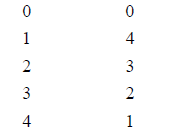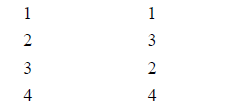
The identity for addition is 0, and the identity for
multiplication is 1. This is a field. We
denote the field of 5 elements by
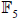
Here is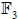 
the finite
field of 3 elements.
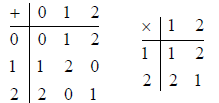
Here is the finite field of 2 elements
.
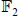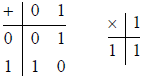
Viewing 0 and 1 as bits, + is just XORing bits, and
multiplication is … well,
multiplication is not too interesting.
The American mathematician E.H. Moore (1862 – 1932) proved
in 1893 that the number
of elements of a finite field must b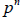e 
for
some prime p and positive integer n, and he
proved that for each prime p and positive integer n there is an essentially
unique field of
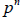elements.
