Objectives
– Verify inverse functions
– Use the horizontal line test to determine if a
function is a one-to-one function.
– Find the inverse of a function.
– Given a graph, graph the inverse .
– Find the inverse of a function & graph both
functions simultaneously .
What is an inverse function?
• A function that “undoes” the original function.
• A function “wraps an x” and the inverse would
“unwrap the x” resulting in x when the 2
functions are composed on each other.
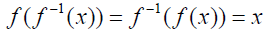
Example
Given that f(x) = 7x − 2, use composition of
functions to show that f−1(x) = (x + 2)/7.
Do all functions have inverses?
• Yes, and no. Yes, they all will have inverses,
BUT we are only interested in the inverses if
they ARE A FUNCTION.
• DO ALL FUNCTIONS HAVE INVERSES THAT
ARE FUNCTIONS? NO.
• Recall, functions must pass the vertical line test
when graphed. If the inverse is to pass the
vertical line test , the original function must pass
the HORIZONTAL line test (be one-to-one)!
One-to-One Functions
A function f(x) is a one-to-one function if
x- values do not share the same y-values.
Remember that a function will have
different x -values.
A one-to-one function will have different
x- values and different y -values.
Why are one-to-one functions important?
One-to-One Functions
have
Inverse functions
Horizontal Line Test
• Use to determine whether a function is
one-to-one.
• A function is one-to-one if and only if no
horizontal line intersects its graph more
than once
Horizontal-Line Test
Graph f(x) = −3x + 4.
Example: From
the graph at the
left, determine
whether the
function is one-to-
one and thus
has an inverse
that is a function.
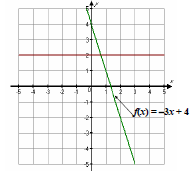
Example:
From the
graph at the
left, determine
whether the
function is
one-to-one
and thus has
an inverse that
is a function.
How do you find an inverse?
• “Undo” the function.
OR
• Replace the x with y and solve for y .
How to find the Inverse of a
One-to-One Function
1. Replace f(x) with y in the equation.
2. Interchange x and y in the equation.
3. Solve this equation for y .
4. Replace y with f-1(x).
Any restrictions on x or y should be considered and
included with the equation.
Remember: Domain and Range are interchanged
for inverses.
Example
Determine whether the function f(x) = 3x − 2
is one-to-one, and if it is, find a formula for
f -1(x).
• The graph of a function and
its inverse always mirror
each other through the line
y=x.
• Example:y = (1/3)x + 2 and
its inverse = 3(x-2)
• Every point on the graph
(x,y) exists on the inverse
as (y,x) (i.e. if (-6,0) is on
the graph, (0,-6) is on its
inverse.
Graph of Inverse f-1 function
• The graph of f-1 is obtained by reflecting the
graph of f across the line y = x.
• To graph the inverse f-1 function:
Interchange the points on the graph of f to
obtain the points on the graph of f-1.
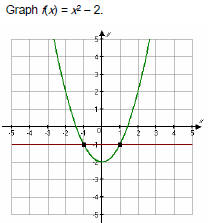
Example
Graph f(x) = 3x − 2 and 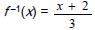
using the same set of axes.
Then compare the two graphs .
Determine the domain and range of the function
and its inverse.
• If a function is one-to-one, then its
inverse is a function.
• The domain of a one-to-one function f is
the range of the inverse f-1.
• The range of a one-to-one function f is
the domain of the inverse f-1.
• A function that is increasing over its
domain or is decreasing over its domain
is a one-to-one function.
Restricting a Domain
• When the inverse of a function is not a
function, the domain of the function can
be restricted to allow the inverse to be a
function.
• In such cases, it is convenient to consider
“part” of the function by restricting the
domain of f(x). If the domain is restricted,
then its inverse is a function.
Restricting the Domain
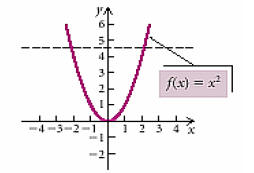
Recall that if a function is not one-to-one,
then its inverse will not be a function.
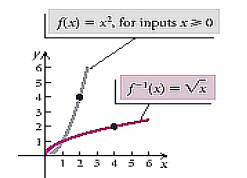
If we restrict the domain values of f(x) to those
greater
than or equal to zero , we see that f(x) is now one-to-one
and its inverse is now a function.
Example
• For f(x) = x² - 1, x < 0:
a.) Find the equation for the inverse , f-1
b.) Find the domain and range for the function and its
inverse.



