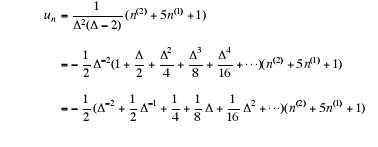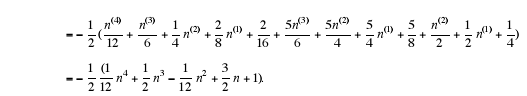Many probability computations can be put in terms of recurrence relations that
have to be satisfied by suc-
cessive probabilities. The theory of difference equations is the appropriate
tool for solving such problems.
This theory looks a lot like the theory for linear differential equations with
constant coefficients.
In order to simplify notation we introduce the forward shift operator E, that
takes a term un and shifts the
index one step forward to un+1.We write
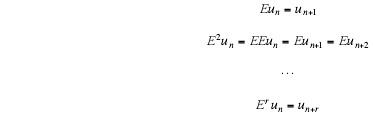
The general linear difference equation of order r with constant coefficients is
where Φ(E) is a polynomial of degree r in E and where we may assume that the
coefficient of E' is 1.
2. Homogeneous difference equations
The simplest class of difference equations of the form (1) has f(n) = 0, that is
simply
These are called homogeneouse quations.
When Φ(E) =(E-λ1)(E-λ2)...(E-λr) where the λi are constants that are all
distinct from each other,
one can prove that the most general solution to the homogeneous equation is
where a1,a2,...,ar are arbitrary constants.
When Φ(E) contains a repeated factor (E-λα)h ,the corresponding part of the
general solution becomes
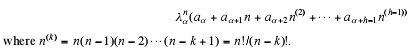
In order to find the n'th term of a linear difference equation of order r, one
can of course start by r initial
values, and the solve recursively for any given n. Thus, if we want our solution
to satisfy certain initial conditions
we may first determine the general solution, and then (if possible) make
it satisfy the initial conditions. There
can be no more than r such initial conditions, but they need not
(as when we compute the solution recursively)
necessarily be conditions on μ0,... ,μr-1,but can be on any set
of r values.
Example 1. Solve μn+2-μn = 0.
The equation can be written in the form
or
The general solution is therefore
where a, b, c are constants.
Example 2. Find the general solution to the equation
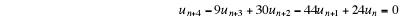
and hence obtain the particular solution satisfying the conditions
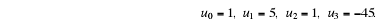
The equation may be written in the form
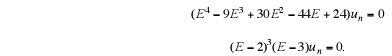
The general solution is therefore
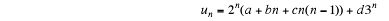
where a, b, c, d are constants.
For the particular side conditions we have
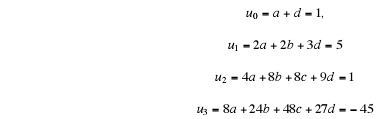
whence a = 0, b =1, c = -2, d =1, so the particular solution is
3. Non-homogeneous difference equations
When solving linear differential equations with constant coefficients one first
finds the general solution for
the homogeneous equation, and then adds any particular solution to the
non-homogeneous one. The same
recipe works in the case of difference equations, i.e. first find the general
solution to
and a particular solution to
and add the two together for the general solution to the latter equation. Thus
to solve these more general
equations, the only new problem is to identify some particular solutions. We
will only give a few examples
here, not attempting to treat this problem in anygenerality.
(i) f(n) = kμn , μ ≠λi, i =1, 2,... ,r
In this case one can show that
is a particular solution to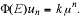 
Let namely
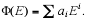Then
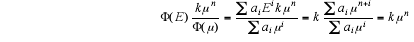
Example 3. The general solution of
is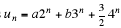 
where a and b are arbitrary constants.
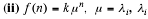a non-repeated factor of Φ(E)
In this case a particular solution is given by
where Φ'(μ) denotes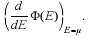 
Example 4. The general solution of
is
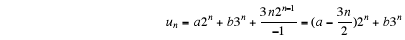
where a, b are arbitrary constants.
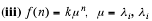a repeated factor of Φ(E)
Suppose now that (E-λi) is repeated h times in Φ(E). Then
where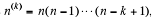 
is a particular solution of the
equation Φ(E)μn=kμn
Example 5. The general solution of the equation
is
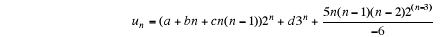
with a, b, c, d are arbitrary constants
(iv) f(n) is a polynomial in n
First write ƒ as a polynomial in the factorial powers n (k) ,so
Now define the difference operator , by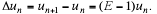 
Using
the symbolic relationship
E=1+Δ we can re-express Φ(E) as Ψ(Δ) Still arguing
symbolically,aparticular solution is obtained by
provided that we can make any sense out of 1/Ψ(Δ) The way this will be
done is by expanding 1/Ψ(Δ)
in powers of Δ and using long division . The following rules are needed :
Δn(r)=rn(r-1)
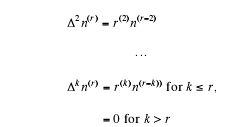
and
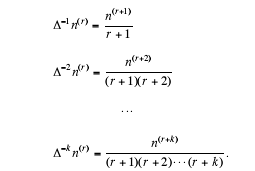
Example 6. Find a particular solution of the equation
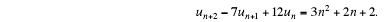
First write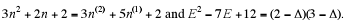 
Thus we
get
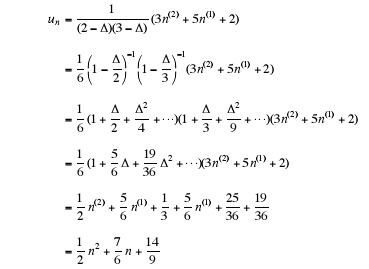
Example 7. Find a particular solution of the equation
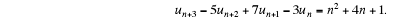
The required solution is
