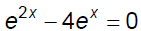Topic 5-4: Solving Logarithmic Equations
A logarithmic equation is an equation involving one
or more logarithmic expressions.
Logarithmic equations can be divided into two
families :
1. Those equations that can be simplified into the form
of a logarithmic expression equal to a number .
2. Those equations that can be simplified into the form
of two logarithmic equations (same base) equal to
each other.
To solve the first case, apply the following steps :
1. Use the laws of logarithms , as necessary, to
combine logarithms .
2. Rewrite the logarithm equation into exponential
form.
3. Solve using any appropriate algebraic and/or
arithmetic methods.
4. Check your solutions. Like radical equations ,
logarithmic equations can (and often do) produce
extraneous solutions.
Ex. 1 Solve.
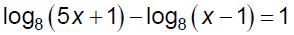
Ex. 2 Solve.
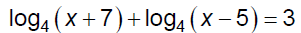
Ex. 3 Solve.
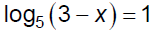
Ex. 4 Solve.
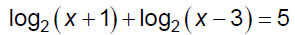
If the equation is simplified (using the laws of
logarithms) in such a way both sides have a
logarithmic expression, consider the limited
possibilities for making the equation true...
Ex. 1 Solve.
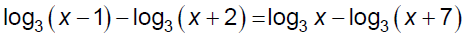
Ex. 2 Solve.
log(x + 4) + log(x + 5) −log(1− x) = log(x + 7)
Topic 5-5: Solving Exponential Equations
An exponential equation is an equation involving
one or more exponential expressions.
Basic process to solve most exponential
equations:
1. Isolate an exponential expression on one side .
2. Take the natural logarithm (or common log) of both
sides.
3. Use the laws of logarithms to rewrite the exponential
expression so that no variable remains in the
exponent.
4. Apply basic algebraic and arithmetic manipulation to
solve for x.
5. Use the laws of logarithms to simplify the solution
and approximate the solution.
6. Check your solution.
With regards to step 5, I will expect you to further rewrite
the solution into a single logarithmic expression and
approximate five places after the decimal .
Ex. 1 Solve.
63x = 100
Ex. 2 Solve.
4 + 3x-2= 16
Ex. 3 Solve.
52x-1 = 18
Ex. 4 Solve.
102x+1 = 500
Ex. 5 Solve.
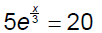
Exponential equations involving 2 exponential
expressions
If the bases are equal or the bases are both powers
of the same constant, solving the equation is fairly
easy.
Ex. 1 Solve.
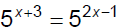
Ex. 2 Solve.
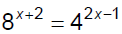
If the bases are neither equal nor related, revert
back to the previously covered process for solving
exponential equations but more or less ignore step
1.
Ex. 1 Solve.
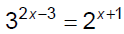
Ex. 2 Solve.
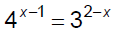
Ex. 3 Solve.
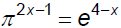
Exponential equations solved by substitution and
factoring
The important skill to remember here is
that 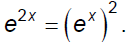
Ex. 1 Solve.
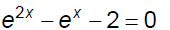
Ex. 2 Solve.