Given a decimal expansion
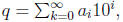where a0 is a non- negative integer ,
and 0 ≤ ai ≤ 9 for all i > 0, we say that q has period t if there exists
an integer s such that ai = ai+t for all i > s. For
example, the decimal
expansion
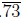has period 2. Here we want to examine the
periods of integers.
Write a program for your calculator or a computer
spreadsheet that does
long division of integers . In particular, it should calculate the nth digit
after the decimal of the decimal expansion for a/b (where a < b are positive
integers) and give you its period.
While writing this program, think about what \bringing
down a zero "
means. Also think about what portions of the algorithm repeat themselves.
Using this program, do questions 1-3, 11, and 12 on page
31 of the class
notes.
Important: There is a typo on problem three. It
should read: nd the least
positive integer kn such that n divides
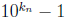if such
an integers exists.
Homework #2
Due Friday, September
I. Problems 1,2,3,5,6,7, 11, 12, 14.
II. Solve the following: In a certain town, two-thirds of the men are married
and two - fifths of the women are married. Assuming all marriages are
between one man and one woman (and everyone is monogamous), what
fraction of the people in the town are married? What are the key ideas
in the solution of this problem ? Can you make your \proof" simple ?
Now, find a student that is not in the sciences (ideally someone who has
not taken calculus), and try and help them solve the problem . Reflect
upon their difficulties (if any) in solving the problem . Also explain
how you helped them work through the problem. (This portion of the
response should be well-written, spell-checked, and make sense.)
