The following is a review of the concepts you should know for this exam. This
review is a sample and is not intended to mirror the exam questions. Any
problems
similar to those discussed in class or in assigned homework may also be assessed
on
the exam.
1. Given f(x) = 2x2, g(x) = 4 - 3x and j(x) = 2x - 5, find
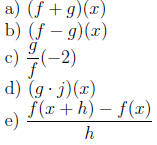
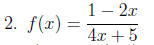
a) Find f(-3)
b) If f(x) = -1/3, find x.
c) What is the domain of f(x)?
d) Find the x-intercept(s).
e) Find the y-intercept.
3. Given the complete graph of f (x):
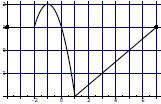
a) What is the domain? What is the range?
b) Find f(3) - f(1).
c) For what values of x does f(x) = 0?
d) Sketch the graph of -f(x + 2).
4. Given the graph of g(x):
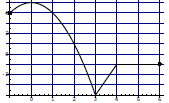
a) List the intervals over which g(x) is increasing, decreasing, or constant.
b) List the coordinates of the local maxima and local minima, if any.
5. Sketch the graph of
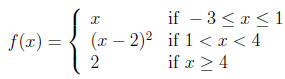
Find:
a) f(-2)
b) f(5)
c) What is the domain of f?
6. Sketch the graph that results from transforming f(x) = |x| by stretching
verti-
cally by a factor of 2 and shifting 3 units up.
7. Use a graphing calculator to nd the real zeros (if any) and the local maxima
and local minima for the function below. Round to two decimal places if needed.
f(x) = -.35x4 + 1.48x3 - 1.75x + 2.62
8. A wire of length x is bent into a square. Express the area of the square as a
function of x.
9. Suppose that an open box with a rectangular base is to be made from a rect-
angular piece of cardboard 18 inches by 14 inches by cutting out a square from
each corner and turning up the sides.
a) Express the volume V of the box as a function of the length x of the side of
the square cut out from each corner.
b) Find the volume if a 4 inch square is cut out.
10. Suppose that the quantity supplied S and quantity demanded D of baseball
caps at a major league game are given by the functions S(p) = 2940 -100p and
D(p) = 110p, where p is the price. Find the equilibrium price for caps at the
game. Then nd the equilibrium quantity.
11. Fantastic Fone, Inc. charges an access fee of $19.95 plus $4.32 per minute
for
each minute after the rst three minutes on all international calls. Express the
total charges, C, incurred as a function of the number of minutes , x, used for a
phone call to London.
12. The volume of water produced from melting snow varies directly as the volume
of snow. Meteorologists have determined that 250 cubic centimeters of snow
will melt to 28 cubic centimeters of water. How much water does 1200 cubic
centimeters of melting snow produce?
13. Use factoring to find the real and complex zeros of the quadratic function.
List
the x- intercepts of the graph of the function.
a) f(x) = 3x2 - 4x - 15
b) g(x) = 25x2 - 1
c) h(x) = 2x2 - 4x
14. Find the real and complex zeros of the quadratic function using the Square
Root Method . List the exact x-intercepts of the graph of the function.
a) f(x) = 4(x + 3)2 - 25
b) g(x) = -3(x - 2)2 - 1
15. Find the real and complex zeros of the quadratic function by completing the
square. List the exact x-intercepts of the graph of the function.
a) f(x) = x2 - 14x + 41
b) g(x) = 2x2 - 6x + 15
16. Find the real and complex zeros of the quadratic function using the
quadratic
formula. List the exact x-intercepts of the graph of the function.
a) f(x) = 2x2 + 10x + 5
b) g(x) = 3x2 - 6x - 7
17. Use u- substitution to transform the function into quadratic form. Then nd
the
zeros of the function. List the exact x-intercepts of the graph of the function.
a) f(x) = (1 - 7x)2 - 2(1 - 7x) - 8
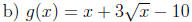
18. Simplify the following expressions with complex numbers:
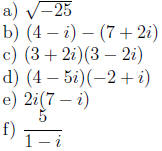
19. If the discriminant (b2 - 4ac) of the quadratic formula is less than zero,
the
nature of the solution (s) is(are):
a) Two unique real solutions
b) One repeated real solution
c) Two complex solutions
d) no solution
20. The graph of f(x) = mx + b is increasing if
a) m < 0
b) m > 0
c) b > 0
d) never increasing
21. Compared to the graph of f(x), the graph of g(x) = f(x + 4) is shifted
a) down 4 units
b) up 4 unites
c) right 4 units
d) left 4 units
22. To complete the square for x2 - 6x, you would
a) add 6
b ) add 9
c) subtract 9
d ) add 1



