Due: Tuesday, September 23rd(at the beginning of
class)
Directions:
1. Complete the following on separate sheets of paper.
2. Full and clear explanations are critical.
3. Staple this sheet to the front of your homework submission.
4. Start Early! If you get stuck, see me during office hours, visit
the Math Tutoring Lab, or
contact someone from class for help.
Refer to the Homework and Quiz Policies we agreed to in
class for questions
about late homework or grading.
Required: Complete all of the following 11 items.
1. Mark is offered the choice of a third of a pizza or a half of a pizza. Since
he is hungry and likes
pizza, he chooses the half. His friend Jane gets a third of a pizza but ends up
with more than
Mark. How can that be? Explain how this riddle can be used to illustrate one or
more ideas
related to fractions that often cause difficulties for students.
2. Explain how to go about writing 5,340,124 in both the
Babylonian and Egyptian numeration
systems . Include both the process you use and the solutions you develop.
3. Suppose five youngsters are given seven brownies to
share. Using words and drawings, explain a
way these youngsters can share the brownies without using fractions. Repeat if
the youngsters
were given only three brownies.
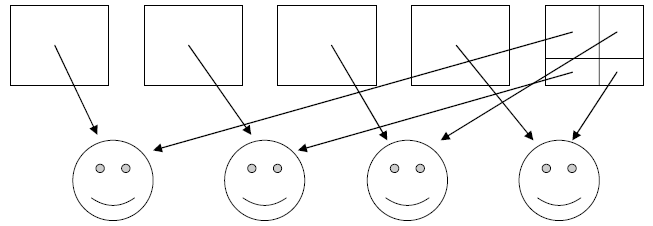
4. Jesse is asked how to share 5 brownies among 4 people.
Jesse responds with the drawing
below. What might you say to Jesse about the method he uses? Be sure to explain
both
the method you think Jesse uses to share and the method that is equivalent to
sharing
using fractions.
5. Convert 17/3 to a mixed fraction and use a drawing to
justify your result. Be sure to label
relevant quantities in your drawing.
6. Draw two-color counters to represent the following
integers in three different ways for
each integer.
a. -3
b. 5
c. -2
d. 0
7. I have 6 units, 13 longs, and 3 cubes . Who am I?
8. I am 256. I have 4 longs. How many units could I have?
9. I am 432. I have 22 units. How many longs could I have?
10. Show 4519 with its minimal collection of base-ten
pieces. Then, show 4519 in four
additional ways with the base-ten pieces.
11. What questions do you have from what we’ve worked on
over the past week or two?
Choices: Choose and complete any 3 of the following 5
items.
1. Suppose a teacher only has decimal blocks to use for an upcoming unit with
fractions.
How might this teacher use units, longs, flats, and cubes to help their students
learn about
ways of representing fractions? Refer to ideas such as sharing, parts of a
whole, and
using different wholes in your description.
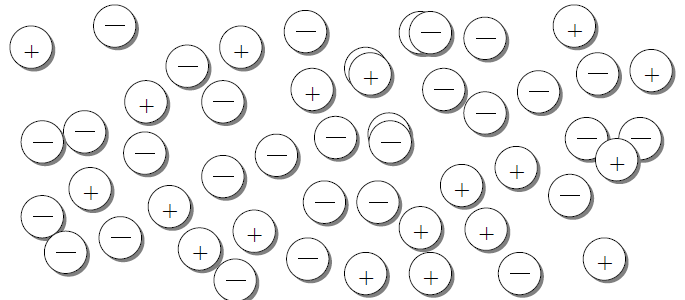
2. Consider the following collection of two-color
counters. In particular, notice that a few of the
counters were accidentally covered. What might be the combined value of the
collection ? Explain
your methods for calculating both (a) the known value of the counters and (b)
the unknown
quantity.
3. Find as many ways as you can to represent 2548 using
exactly 28 base-ten pieces.
Explain your answers.
4. Draw a picture of 20 two-color counters that
collectively represent a value of -6. Then,
describe the possible values that can be obtained by flipping exactly two or
exactly three
of the counters. Explain your thoughts about possible outcomes using full
sentences.
5. Choose either Pattern Blocks or Cuisenaire Rods. Then,
use drawings and words to
describe at least 3 ways the manipulatives you chose can be used to represent
fractions. In
particular, discuss how to use your manipulatives to express equivalent
fractions.



