This is a take-home "pretest" to test your math background
for this
course. It will be graded! However, if you don't see an answer to a question,
you are free to ask a friend for help, or use a book or the web as a resource.
Please show all your work.
This test will be used for two purposes : 1) to divide the class up into
groups which are roughly balanced in terms of mathematical background
(the class project and at least some hws will be done in groups) and 2) to
see how much math review we need to do in class.
Graded Problems:
1. Find the solutions to this equation : x2 - 5x - 14 = 0.
Solution: (x - 7)(x + 2) = 0, in other words, x = 7 or x = -2.
Can solve this by "eyeballing" the equation or by using the quadratic
formula (see below)
2. Find the solutions to this equation x 2 - x - 1 = 0
Solution: For equations of the form: ax2 + bx + c = 0, we can use
the quadratic formula: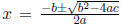 . The equation above can be
. The equation above can be
written: 1x2 -1x-1 so a = 1, b = -1, c = -1. Plugging this into the
quadratic formula, we get 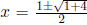 . So one solution
is
. So one solution
is 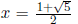
and the other is 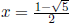
3. Assume that x+y = 7 and -2x+2y = 2 for unknown variables x and
y. What are the values of x and y ?
Solution: To solve this, use the linear algebraic trick for solving two
equations in two unknowns (to be shown in class). The answer is
x = 3, y = 4
4. Assume you know that some function f is of the form
f(x) = ax2+bx,
where the coefficients a and b are unknown . Assume further that
f(1) = 2 and f(2) = 10. What are the coefficients a and b?
Solution: f(1) = 2 implies that a + b = 2, f(2) = 10 implies that
4a + 2b = 10. So we have two equations and two unknowns, and we
can solve for a and b to get a = 3, b = -1. Thus, the unknown
function is f(x) = 3x2 - x
5. For each of the following equations, say whether it is always true, or
if it may be false. If the equation is always true, say why. If it's
false, give values for which it is false. All logs are base 2 unless stated
otherwise.
(a) 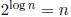 Solution: True by defn of log
Solution: True by defn of log
(b) 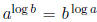 . Solution: True since
. Solution: True since
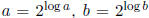 , and if
, and if
we replace these quantities in the equation, we get the equation
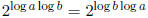 which is trivially true
which is trivially true
(c) 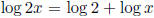 Solution: True since
Solution: True since
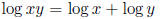
for any x and y
(d)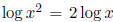 Solution: True since
Solution: True since
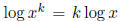 for any k
for any k
and x
(e) 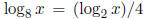 (that is, log base 8 of x is log base 2 of x
(that is, log base 8 of x is log base 2 of x
divided by 4.
Solution: False: This is false for x = 8. The correct equation is
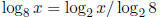 which reduces to
which reduces to
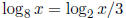
6. What is 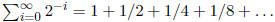
Solution: Let 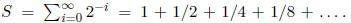 Then
Then
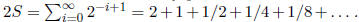 Subtracting the first
Subtracting the first
equation from the second, we get S = 2
7. Prove, by induction on n, that 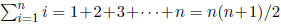 .
.
Solution: B.C. 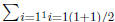 . Now assume, by the inductive hypothesis
. Now assume, by the inductive hypothesis
that 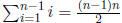 . Then
. Then
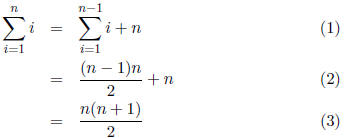
8. Prove, by induction on n, that
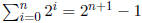
Solution: B.C. 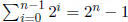 . Assume by the inductive hypothesis
. Assume by the inductive hypothesis
that 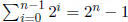 . Then
. Then
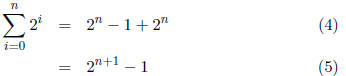
9. Let's say you have 2 blue blocks, and 2 green blocks,
and 1 red block
that are otherwise indistinguishable. How many different columns of
height 5 can be built from these 5 blocks? For this problem, BRBGG
and GGBRB will be considered to be two different columns (i.e. there
is a bottom up ordering ).
Solution: There are 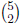 places to put the blue blocks initially. Then,
places to put the blue blocks initially. Then,
there are three places remaining to put the red block, and the column
is complete. So the total number of columns is
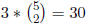
Ungraded Questions:
1. If there are any students in the class who you'd prefer to work with,
or prefer not to work with, please list them here (every e ort will be
made to honor these requests):
Prefer to work with:
Prefer not to work with:
2. Put an "X" in any slot when you are normally
unavailable to work on
homeworks and projects i.e. the times when you have conflicts . (This
info will be used to try to put you in a group with a compatible time
schedule)
| |
Mon |
Tues |
Weds |
Thurs |
Fri |
Sat |
Sun |
| Morning |
|
|
|
|
|
|
|
| Afternoon |
|
|
|
|
|
|
|
| Evening |
|
|
|
|
|
|
|
3. Circle the algorithms and data structures that you
could code in a
language of your choice:
Mergesort  Quicksort
Quicksort
 Linked List
Linked List
 Binary Tree
Binary Tree
 Heap
Heap
4. Circle the languages that you are comfortable programming in:
C C++ Java



