It is important for you
a) To understand the process of Gaussian elimination by
row operations leading to the
possible solutions to a system of linear equations.
b) To understand that a system of linear equations can
have no solutions, one solutions,
or many solutions; and to begin to understand how these different outcomes
occur.
Particularly: how do you recognize which situation you are in, using the echelon
form
of your system.
c) To understand what it means for a system to be
homogeneous, and the rubric “general
= homogeneous + particular”
d) To understand what a field is, and how the fact that
the real numbers form a “field”
plays a role in solving linear equations.
This work sheet will help you to work on two problems.
First, given a, b, c, d, when does
the system
ax + by = i
cx + dy = j
have a unique solution for every pair of numbers i , j?
1. First, suppose I tell you that a ≠ 0. Use this to put
the matrix in echelon form.
2. OK, now that you’ve done that, is y determined by the
second row? Sometimes it is,
sometimes it isn’t. What’s the condition that says it is? What happens if y
isn’t determined
by the second row?
3. In general a may be zero . Suppose it is. We have to
consider two cases: c ≠ 0 and c = 0.
If a = 0 and c = 0, can there be a unique solution for every i and j? Can ad−bc
be non-zero?
4. Finally we’ll consider the case that a = 0 but c ≠ 0.
Put the matrix in echelon form.
Now what condition says that y is determined by the second row?
The other problem I would like us to consider is problems
I.1 5a and 7b in Halmos.
Actually, we can do them both at the same time. Fix a rational number z with the
property
that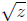
is not a rational number. For example z
= −1 and z = 2. We need to show that
Q(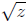
) is a field. This is the set of
expressions
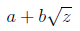
where a, b ∈Q. We add them using the formula
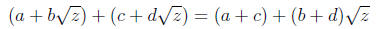
(just like adding polynomials). We multiply them just as
we multiply polynomials too :
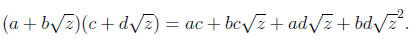
5. Simplify this last expression, so it takes the form
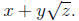
The interesting thing is to show that you can divide by
any non-zero expression. That
is, given a, b and v,w ∈Q with a, b non-zero, there are rational numbers x, y
such that
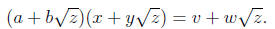
Moreover if v,w are non-zero, the solution
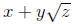is unique. Let’s prove it.
6. Write out the product
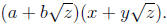Collect the terms without 
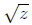and set them
equal to v. Collect the terms with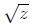
and set
them equal to w.
7. Now you have two linear equations in the two variables
x and y . Apply the condition
“ad − bc ≠ 0” from earlier: what condition do you get?
8. Solve the system of linear equations for x and y.
