1 Complex Numbers
Remember the powers of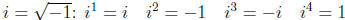 
.
Addition and subtraction are straightforward (well, except when you’ve got
radicals ...but
that’s another story). Add/subtract real parts and imaginary parts separately.
Example: (3 + 2i) + (2 − 3i) = (3 + 2) + (2 − 3)i = 5 + (−1)i = 5 − i
Multiplication is done by FOIL or distributive property.
Example: (3 + 2i)(2 − 3i) = 6 − 9i + 4i − 6i2 = 6 − 5i + 6 = 12 − 5i
Example: 3i(2 + 9i) = 6i + 27i2 = 6i − 27 = −27 + 6i
Division is done by rationalizing the denominator by either multiplying by the
irrational
stuff (including i) or by multiplying by conjugate.
Examples:
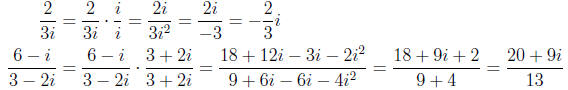
2 Real and Complex Zeros of Quadratic Equations
We can find the real and complex zeros of quadratic equations four different
ways :
1. Factoring (a.k.a. Zero Product Property )
2. Square Root Method
3. Completing the Square
4. Quadratic Formula
2.1 Factoring
This works anytime you have some quadratic equation equal to 0 that factors .
Example: (x + 2)(x + 4) = 15. Notice that no side is equal to zero. That means
we must
FOIL the left-hand side, subtract the 15, and refactor.
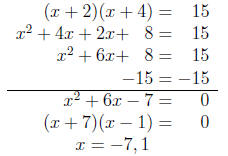
2.2 Square Root Method
This works best when you have (something with x)2 = something else (or you can
rewrite
in that way).
Examples:
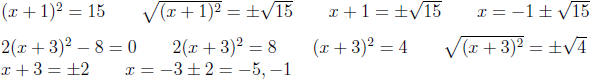
2.3 Completing the Square
This can be done several ways. The last two will serve you well throughout the
whole chapter.
The first one isn’t good for rewriting functions.
2.3.1 Add (b/2)2 to both sides
Example: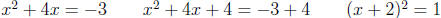 
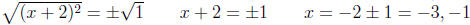
2.3.2 Add and subtract (b/2)2 to one side
Example: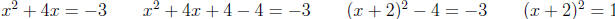 
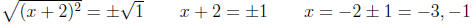
2.3.3 Vertex Point
Example: x2 + 4x = −3
x2 + 4x + 3 = 0. It’s important to get one side equal to
zero to
do this method.
Take f(x) = x2 + 4x + 3 (the side that’s not zero). Then the vertex point is
(−2,−1).
(Remember that
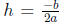and k = f(h).) So f(x) = (x + 2)2 − 1, and we want to find its
zeros. So
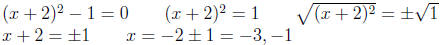
2.4 Quadratic Formula
Simply memorize the formula. Sing it to the tune of “Pop Goes The Weasel” if you
must!
The formula works, though, only if one side is equal to zero! If ax2 + bx + c =
0, we have
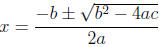
Example: 3x2 + 2x + 1 = 0
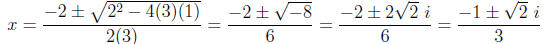
3 Quadratic in Form
The equations have three terms. They should be organized in descending order .
The first
two terms have x’s, and the third is just a number. Observe that the exponent on
the first
x should be twice the exponent of the second.
Examples: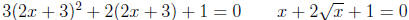 
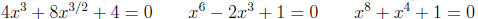
To solve these, convert them to a quadratic by taking
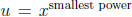. (Or,
if you have
some expression in x raised to a power, take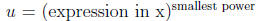
Then rewrite
the x’s (or expressions), with the higher power as u2 and the lower power as u.
Solve as a
quadratic. Then see if the solutions are real . (Hint: Square root = negative #
or square =
negative # are not real.) Finally, take the u = substitution and solve for x.
Substitute your
u solutions into that to get your x’s.
Note that we only talk about real zeros of things that are quadratic in form.
This is because
we won’t get to the whole story about the complex zeros of them in Math 101.
Example: Find the real zeros of f(x) = x6 − 2x3 − 3. So we’re solving the
equation x6 +
2x3 − 3 = 0. Take u = x3. Then u2 − 2u − 3 = 0. By factoring, (u + 1)(u − 3) =
0, so
u = −1, 3. Then, since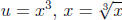 
. We then say that
.
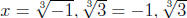Example: Find the zeros of g(x) = (3x + 1)2 − 2(3x + 1) − 3. So we’re solving
the equation
(3x + 1)2 − 2(3x + 1) − 3 = 0. Let u = 3x + 1. Then we solve u2 − 2u − 3 = 0
like we did
above. Its solutions are u = −1, 3. Since u = 3x + 1,
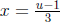. So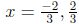 
.
Remark: This last example can be solved like an ordinary quadratic if you don’t
mind doing
all the FOIL and distributive property stuff .
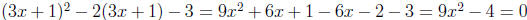. We can do square root
method to solve this one, since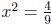 
, so
.
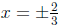