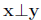Basics
Vectors An array of n real numbers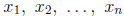 
is
called a vector and it is written
as
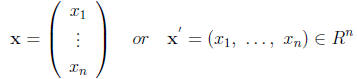
( prime operation =transposing a column to a row)
Basic vector operations
Multiplication with a constant c
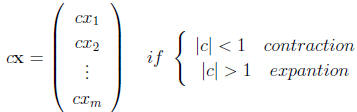
Addition of x, y ∈ Rn
Inner Product or Scalar Product
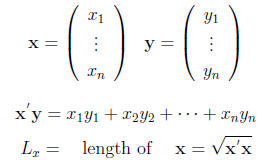
Let x, y ∈ R2 and
denotes the angle between the vector
and the x axis. Then
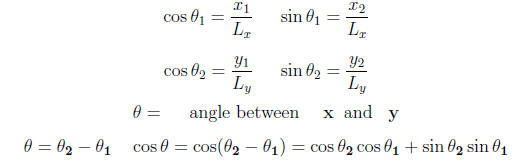
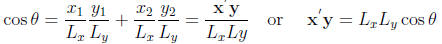
In general for x, y ∈ Rn
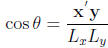
Remark: cos θ= 0
x and y are perpendicular.
Length of a vector x ∈ Rn:
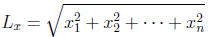
How multiplication with a constant c changes the length ?
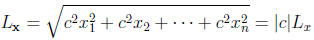
Remarks:
–Let
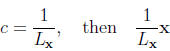
is a vector with unit length and with direction of x.
– If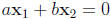 
then 
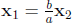and
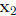have the same
direction but different length .
Unit vectors in R2:
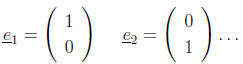
Unit vectors in Rn:
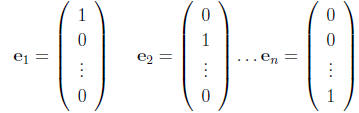
Let
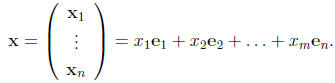
Definition: The space of all n-tuples with scalar
multiplication and addition as defined above,
is called a vector space.
Definition: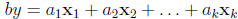 
is a linear combination
of the vectors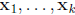 
.
The zero vector is defined as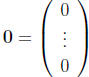 
Definition: The vectors
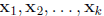are said to be
linearly dependent if there exist k numbers
not all zero , such that
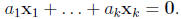
Otherwise 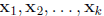is said to be linearly
independent .
Examples:
(i)
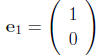and
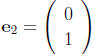are linearly independent , because
if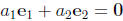 
then
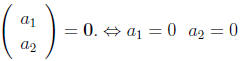
(ii) Similarly you can prove in Rn that
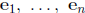are
linearly independent .
(iii) Let
Then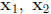 
and
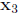are linearly dependent since
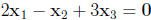
Definition: A set of m linearly independent vectors in Rm called a basis for the
vector space
of m-tuples.
Theorem: Every vector in Rm can be expressed as a unique linear combination of a
fixed
basis.
Example Let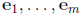 
be a basis in Rm. Then
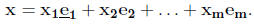
Definition: The length of a vector x is
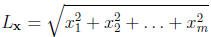
Definition: The inner product or dot product of two
vectors x, y ∈ Rm is
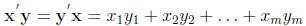
Remark:
(i) Length of a vector x:
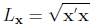
(ii) Let us denote θ the angle between two vectors x,
y ∈ Rm. Then
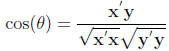
Definition: When the angle between two vectors x and y is
θ = 90°or 270°we say that x
and y are perpendicular or orthogonal
Since cos 90°= cos 270°= 0 x and y are perpendicular if x'y = 0.
Notation 
