Thu. 11/6 Agenda:
* Review HW for Sec. 7.6
* Begin 7.7 on quadratic equations , incl. 4 methods of solving.
Sec. 7.7 HW #1-4, 9-35 odd, 37-48 all

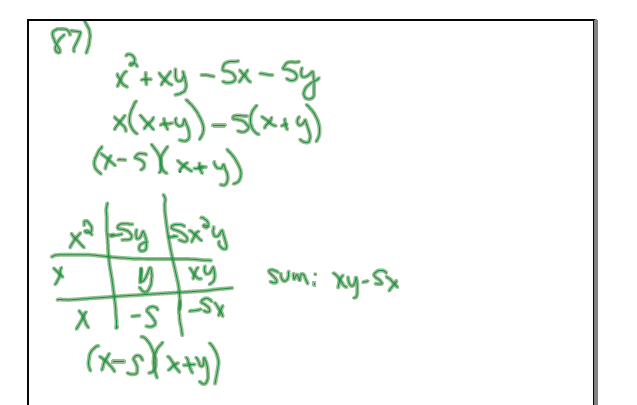
Solving Quadratic Equations
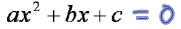
Four Methods :
1. Factoring,
2. Square Root Method,
3. Completing the Square, and
4. Quadratic Formula
Each method works better for certain kinds of problems.
Method 1: Factoring and the ZPP
The ZPP ( zero product principle ) states:
If ab = 0, then either a = 0 or b = 0.

Method 2: Square Root Method
The SRP (square root principle) states:
If x^2 = k and k≥0, then the two solutions are 
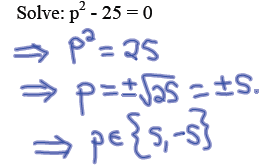
Method 2: Square Root Method
The SRP (square root principle) states:
If x^2 = k and k≥0, then the two solutions are 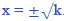
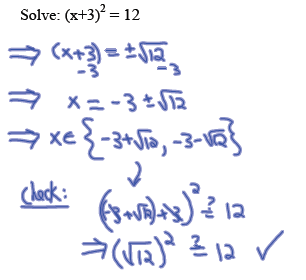
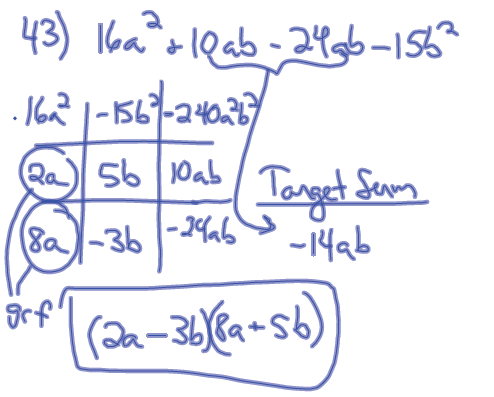
Method 3: Complete the Square
A perfect square trinomial (PST) has the form
(x+d)^2 = x^2 + 2dx + d^2.
Which of the following are PST's?
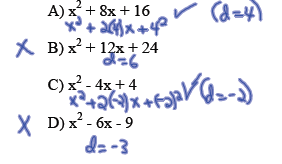
Method 3: Complete the Square
A perfect square trinomial (PST) has the form
(x+d)^2 = x^2 + 2dx + d^2.
Make the following into PST's.
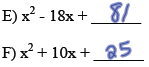
Describe your process.
Method 3: Complete the Square
A perfect square trinomial (PST) has the form
(x+d)^2 = x^2 + 2dx + d^2.
Solve by 1) completing the square to form a perfect square
trinomial and then 2) applying the square root principle:
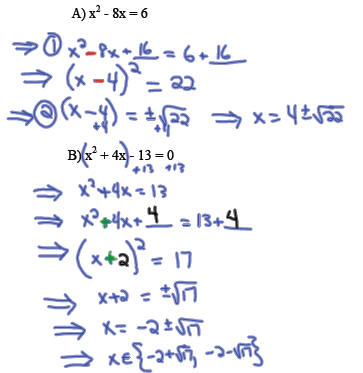
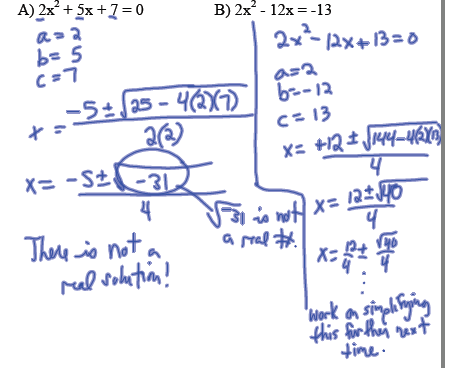
Method 4: The Quadratic Formula :
If ax^2 + bx + c = 0, then the two solutions are :

(Proof is based on completing the square).
Before we practice, let's review what we have so far:
Method 1: Factor and use ZPP
Method 2: Use the Square Root Principle
Method 3: Complete the Square, then use Method 2.
Method 4: Use the Quadratic Formula , then Simplify .
PS4 #4 asks you to reflect on the types of problems that
are best
handled by each of these methods.
For instance, the Quadratic Formula "always works," but it
is cumbersome and may not be the best approach in all cases.
Method 4: The Quadratic Formula:
If ax^2 + bx + c = 0, then the two solutions are:
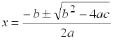
Solve using the quadratic formula: