Objectives: To solve quadratic equations by :
1. Square Root Property
2. Completing the square.
3. Using the Quadratic Formula
4. To use the discriminant to indicate the type
of solutions for the quadratic equation.
5. To find the x and y intercepts of a
quadratic function.
6. To solve application problems.
Quadratic equation-a second degree equation in one
variable, containing a variable with an
exp onent of 2.
ax2 + bx + c = 0-standard form.
Example: Solve:
1. x2 = 81
There is another way to solve this equation. Notice that
the solutions are numbers that can be squared to equal 81. These numbers are the
square roots of 81, which are 9 and -9.
Let’s state this as a rule .
The Square Root Principle
For any real number a, x2 = a if and only if
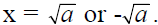
Solve:
Now lets use this property to solve equations in the form x2 = a.
Solve:
1. x2 = 121
2. x2 = 45
3. x2 + 9 = 0
4. 5n2 = 12
5. 2x2 + 11 = 65
6. ( x – 4)2 = 18
7. 2(x – 3)2 – 8 = 22
SOLVE BY COMPLETING THE SQUARE.
1. x2 + 8x +15 = 0
Solving a quadratic by Completing the Square
To solve a quadratic equation by completing the square:
1. Write the equation in the form x2 + bx = c
2. Complete the square by adding (b/2)2 to both sides.
3. Write the completed square in factored form .
4. Use the square root principle to eliminate the
square.
5. Isolate the variable.
6. Simplify as needed .
Solve each of the fol lowing by completing the square:
1. x2 – 12x – 5 = 0
2. 9x2 + 18 x = -1
Instead of completing the square on each problem, let’s
complete the square on the general quadratic equation and derive a formula.
Let’s derive the Quadratic Formula
ax2 + bx + c = 0
Quadratic Formula
ax2 + bx + c = 0 if and only if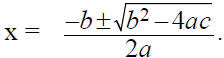
Now let’s use it to solve:
1. x2 + 3x – 8 = 0
a = _____ b = _____ c = _____
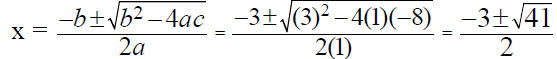
2. x2 – 9x = 41
First you must write your equation in the correct form.
______________ =0
a = ___ b =___ c = ___
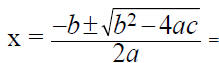
3. 3x2+ 10x = 8
a = ____ b = ____ c = _____
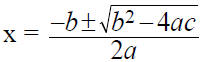
Choosing a method for Solving Quadratic Equations
We have now studied several methods for solving a
quadratic equation. The following table summarizes the methods .
| Method |
When the Method is Best |
| 1. Factoring |
If the quad. can be factored easily |
| 2. Square Root |
If quad can easily be written in ax2 = c or (ax
+ b)2 = c |
| 3. Completing the square |
Rarely used |
| 4. Quadratic formula |
When factoring is not easy. |
The expression b2 – 4ac is called the discriminant.
Given a quadratic equation in the form ax2 + bx + c = 0, where a ≠ 0, to
de termine the number and type of solution the quadratic has we will evaluate the
discriminant. If
b2 –4ac < 0, then the equation has two non real
( complex )
solutions
b2 –4ac = 0, then the equation has one real solution
b2 –4ac > 0, then the equation has two real solutions.
Find the value of the discriminant, and use it to
determine the number and type of solutions.
1. x2 + 7x – 3 = 0
b2 –4ac
2. x2 – 8x + 16 = 0
b2 –4ac
3. x2 + 6x + 18 = 0
b2 –4ac
Graph of f (x) = ax2 + bx + c
When we graph a quadratic function three “nice” points are
the x and y intercepts.
Remember to find the x intercept we let y = 0, and to find the y intercept we
let x = 0.
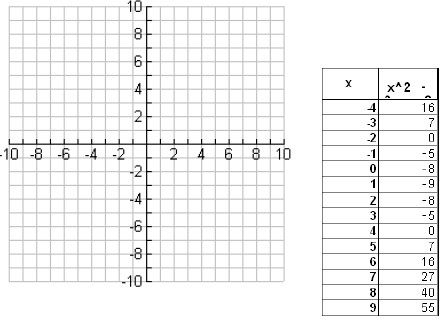
Graph y = x2 - 2x - 8 by first finding the x and y
intercepts.
1. Let y = 0
0 = x2 - 2x - 8
0 = (x - 4)(x + 2)
The x intercepts are ___________ and _________
2. Let x = 0
y = (0)2 - 2(0) - 8 =
The y intercept is _____.
Now let’s make a table and graph this function.
Problem Solving
Translate to a quadratic equation, then solve.
1. The length of a rectangular floor is 2 meters less than
three times its width. If the area is 96 meters, find the length and width.
2. On a 135 mile bicycle excursion, Maria averaged 5 mph
faster for the first 60 miles than she did for the last 75 miles. The entire
trip took 8 hours. Find her rate for the first 60 miles.
3. Using a riding mower, Fran can mow the grass in 4 hours
less time than it takes Donnie using a push mower. Together they can mow the
grass in 2 2/3 hours. How long does it take each working alone?
| Worker |
Time
alone |
Rate of
work |
Time at
work |
Portion of job com |
| Fran |
x - 4 |
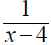 |
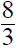 |
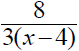 |
| Donnie |
x |
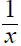 |
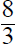 |
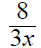 |



