Graphs of Quadratic Functions
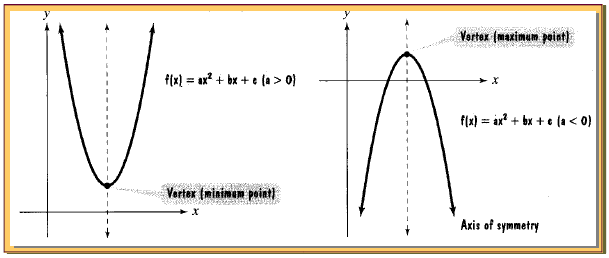
The graph of any quadratic function is called a parabola.
Parabolas are shaped like cups, as shown in the graph below. If
the coefficient of x 2 is positive, the parabola opens upward;
otherwise, the parabola opens downward. The vertex (or turning
point) is the minimum or maximum point.
The Standard Form of a
Quadratic Function
• The quadratic function
• f (x) = a( x - h)2 + k, a ≠ 0
• is in standard form. The graph of f is a parabola
whose vertex is the point (h, k). The parabola is
symmetric to the line x = h. If a > 0, the parabola
opens upward; if a < 0, the parabola opens
downward.
Graphing Parabolas With Equations
in Standard Form
• To graph f (x) = a(x - h)2 + k:
2. Determine whether the parabola opens upward or
downward. If a > 0, it opens upward. If a < 0, it opens
downward.
3. Determine the vertex of the parabola. The vertex is (h,
k).
4. Find any x-intercepts
by replacing f (x) with 0. Solve
the resulting quadratic equation for x .
5. Find the y-intercept
by replacing x with zero .
6. Plot the intercepts and vertex. Connect these points with
a smooth curve that is shaped like a cup.
Text Example
• Graph the quadratic function f (x) = -2(x - 3)2 + 8.
Solution We can graph this function by following the steps
in the preceding
box. We begin by identifying values for a , h, and k.
| Standard form |
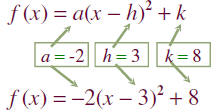 |
| Given equation |
Step 1 Determine how the parabola opens. Note that a, the
coefficient of
x 2, is -2.Thus, a < 0; this negative value tells us that the parabola opens
downward.
Step 2 Find the vertex . The vertex of the parabola is at
(h, k). Because h =
3 and k = 8, the parabola has its vertex at (3, 8).
Step 3 Find the x-intercepts.Replace f (x) with 0 in f (x) = -2(x - 3)2 + 8.
| 0 = -2(x - 3)2 + 8 |
Find x-intercepts,
setting f (x) equal to zero. |
| 2(x - 3)2 = 8 |
Solve for x . Add 2(x - 3)2 to both sides of
the equation. |
| (x - 3)2 = 4 |
Divide both sides by 2. |
| (x - 3) = ±2 |
Apply the square root method . |
| x - 3 = -2 or x - 3 = 2 |
Express as two separate equations. |
| x = 1 or x = 5 |
Add 3 to both sides in each equation. |
The x- intercepts
are 1 and 5. The parabola passes through (1, 0) and (5, 0).
Step 4 Find the y-intercept.
Replace x with 0 in f (x) = -2(x - 3)2 + 8.
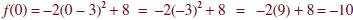
The y-intercept
is –10. The parabola passes through (0, -10).
Step 5 Graph the parabola. With a vertex at (3, 8), x-intercepts
at 1 and 5,
and a y-intercept
at –10, the axis of symmetry is the vertical line whose
equation is x = 3.
The Vertex of a Parabola Whose
Equation Is f (x) = ax2 + bx + c
• Consider the parabola defined by the
quadratic function
• f (x) = ax2 + bx + c. The parabola's vertex is
at
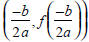
Example
Graph the quadratic function f (x) = -x2 + 6x -2.
Solution:
Step 1 Determine how the parabola opens. Note that a, the
coefficient of x2, is -1.
Thus, a < 0; this negative value tells us that the
parabola opens downward.
Step 2 Find the vertex. We know the x-coordinate
of the vertex is x =
-b/(2a). We identify a, b, and c to substitute the values into the
equation for the x-coordinate:
x = -b/(2a) = -6/2(-1)=3.
The x- coordinate
of the vertex is 3. We substitute 3 for x in the equation
of the function to find the y-coordinate:
y=f(3) = -(3)^2+6(3)-2=-9+18-2=7, the parabola has its vertex at (3,7).
• Step 3 Find the x-intercepts.
Replace f (x) with 0 in f (x) = -x2 + 6x
- 2.
a = -1,b = 6,c = -2
• 0 = -x2 + 6x - 2
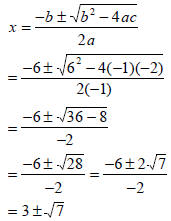
• Step 4 Find the y-intercept. Replace x with 0 in f (x) = -x2 + 6x -
2.
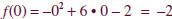
The y-intercept
is –2. The parabola passes through (0, -2).
Step 5 Graph the parabola.
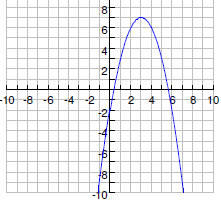
Minimum and Maximum:
Quadratic Functions
• Consider f(x) = ax2 + bx +c.
2. If a > 0, then f has a minimum that occurs at
x = -b/(2a). This minimum value is f(-b/(2a)).
3. If a < 0, the f has a maximum that occurs at
x = -b/(2a). This maximum value is f (-b/(2a)).



