Assumptions: I am assuming in this discussion that
all numbers implied by the use of the fractional
exponents will be REAL NUMBERS. This will become clearer in the next lesson when
I discuss Complex
Numbers that are NOT REAL NUMBERS and do NOT always behave as ”nicely” as real
numbers!
REMINDERS ON NEGATIVE EXPONENTS DO’s and DON’Ts: Things that you CAN DO:
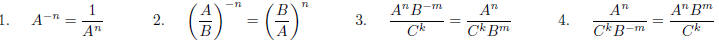
The last three are just a consequence of the basic
relation in #1, but keeping them in mind and being
comfortable working with them will save you from the extra trouble of having to
go through steps with
complex fractions. Now for things you can NOT DO:
WARNING: A NEGATIVE EXPONENT DOES NOT MAKE THE NUMBER NEGATIVE, AND
NEGATIVE NUMBERS HAVE NOT SUDDENLY BECOME FRACTIONS!!!!!!
These are two, unfortunately, not uncommon, but Very Serious Errors that
students make.
For example: 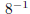 does NOT equal −8 CORRECT:
does NOT equal −8 CORRECT:
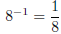
Some have apparently made what I call ”cancelling errors” in their work and
convinced themselves that their
wrong thoughts are correct, for instance, they will have these erroneous steps
on the test:
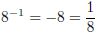 WRONG!!!!!!!!!! Two BAD ERRORS!
WRONG!!!!!!!!!! Two BAD ERRORS!
So, ”Just getting the right answer” is not enough if I see that there are
serious errors in getting to it!
−3 does NOT equal  . These are the same two
numbers that they have always been... How could a
. These are the same two
numbers that they have always been... How could a
negative three equal a positive one − third? Do you see how little sense this
makes? However, I can’t
remember grading a test involving negative exponents that someone didn’t make
these mistakes. You be the
class to start a new trend and learn the difference!
MORE FRACTIONS? - WHAT DO THEY MEAN UP THERE?: This may be what you
are thinking when you see an expression like
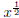 . Our clues to the meaning of this must come
from our
. Our clues to the meaning of this must come
from our
previous knowledge of Exponent Rules (Reviewed in Notes #1). You probably saw
these exponent rules for
the first time years ago, and learned the basics of working with simple whole
number exponents. Then some
time later, perhaps for the first time in MS101, you were introduced to the idea
of the negative exponent
being the same thing as a reciprocal or inverse. But, hopefully, you noticed
that the basic Exponent Rules
DID NOT CHANGE. They had to be consisitent to include the negative integers as
well as the whole numbers.
The same is true now when the idea of a rational or fractional exponent is
introduced .... The basic
EXPONENT RULES for Multiplying together same bases, Dividing same bases, or
Raising a Power to a
Power DO NOT CHANGE!
TRY THINGS OUT: What would happen if we took our expression above,
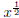 and squared it?
and squared it?
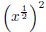 According to our ”Power Rule,” this must:
According to our ”Power Rule,” this must:
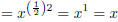
Now, ask yourself, what is it that is squared that gives me back x... It is
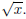
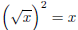 so do you see that we can conclude that:
so do you see that we can conclude that:
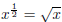 Similarly, we can
conclude that:
Similarly, we can
conclude that:
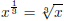 and generally
and generally
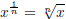 for n a positive integer.
for n a positive integer.
Also to Keep the Basic Exponent Rules consistent, if we had
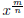 , we would notice:
, we would notice:
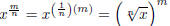 Also:
Also:
EQUATION #2: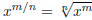 This is better for use in
equations because it looks neater.
This is better for use in
equations because it looks neater.
However, for evaluating numbers the first one is better because it keeps the
numbers that you have to work
with smaller.
EVALUATE USING EQUATION #1 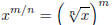 : To
EVALUATE means to find the
: To
EVALUATE means to find the
value of , so in the first excercises and on the Worksheets, you will be getting
used to this new exponent by
literally finding out what the value of things like 641/2 is. Use the above
formula and proceed, but try to
learn to start thinking in the language of fraction exponents ... New notation
is just like a foreign language
and when you learn to ”think” in the new language, you don’t have to go back
through the ”translation”
process.
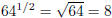 Now try:
Now try:
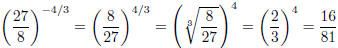
You can see that you needed the previous knowledge about
negative exponents ”making inverses” to be able
to do this problem.
WARNING: Notice that the Negative Exponent did NOT indicate taking an inverse of
the exponent:
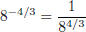 CORRECT
CORRECT
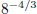 does NOT equal
does NOT equal
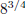 WRONG!!!!!!!!!!!
WRONG!!!!!!!!!!!
EXPONENT TO RADICAL FORM : Use Equation #2 to change an expression or
equation from
rational exponent form to radical form ... it looks neater than the Equation #1
form. What you have to be
CAREFUL of here is Order of Operations . For example:
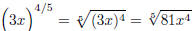 BUT:
BUT:
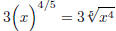
WORK WITH RATIONAL EXPONENTS: In problems where you
are told to express your results
using positive exponents only, the idea is to USE THE EXPONENT RULES — NOT TO
CHANGE
BACK TO RADICAL FORM! On these problems, changing back to radical form will, in
general, just cause
trouble and not be a help.
EXAMPLES: Simplify , using exponent rules, do NOT leave any negative or zero
exponent in your answer:
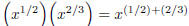 NOTE: We have just applied our exponent rule
that says to add exponents when
NOTE: We have just applied our exponent rule
that says to add exponents when
we multiply the same base. Do your scratch work and add: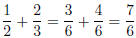 ,
so our Final Answer:
,
so our Final Answer:
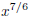
The other problems are worked in similar ways, in that you apply the appropriate
exponent rule(s) for multiplication,
division, and powers, as needed. The only difference to problems that you have
done previously
is that now your arithmetic will involve some fractions, so just be careful!
(Pay attention to the warnings!)



