Solving Equations by Factoring

Definition: The zero- product property says that if a and b are numbers and if ab = 0, then
a = 0 or b = 0 (or both).
Definition: A quadratic equation is an equation that can be written ax² + bx + c = 0,
where a, b, and c are numbers and a ≠ 0.

Solving Quadratic Equations
To solve a quadratic equation, we must find all possible values for x that make ax² + bx +
c = 0. Factoring is usually a helpful way to solve quadratic equations. To use factoring,
move all nonzero terms to one side of the equal sign so that the other side is zero. Then
use the zero- product property .

Examples:
1. Solve the equation x ² – 5x – 24 = 0.
Only the left-hand side (LHS) of the equation has nonzero terms, so no movement
of terms is necessary. Factor the LHS and use the zero-product property (ZPP):

x2 – 5x – 24 = 0
Factor: (x + 3)(x – 8) = 0
ZPP: x + 3 = 0 or x – 8 = 0
Solve for x: x = –3 or x = 8

2. Solve 2x² + 18x – 72 = 0 for x.
All nonzero terms are on the LHS, so no movement of terms is needed.

2x² + 18x – 72
Factor: 2(x + 12)(x – 3) = 0
ZPP: x + 12 = 0 or x – 3 = 0 (Note: 2 ≠ 0, so we don’t write it)
Solve for x: x = –12 or x = 3

3. Solve the equation 6x² – 27x = –12.
This equation has nonzero terms on both sides of the equal sign . To make it
possible to solve, move the –12 to the LHS by adding 12 to both sides:

6x² – 27x + 12 = 0
Factor: 3(2x – 1)(x – 4) = 0
ZPP: 2x – 1 = 0 or x – 4 = 0 (Note: 3 ≠ 0)
Solve for x: x = ½ or x = 4

4. Solve 16x² = 1.
Subtract 1 from both sides: 16x² – 1 = 0
Factor: (4x – 1)(4x + 1) = 0 (Note: This is a ‘special’ polynomial.)
ZPP: 4x – 1 = 0 or 4x + 1 = 0
Solve for x: x = ¼ or x = -¼

5. Solve: –12x² = –17x + 6
This quadratic equation has nonzero terms on both sides of the equal sign, so we
must move all the terms to one side. Add 17x – 6 to both sides and solve.

–12x² + 17x – 6 = 0
Factor: –1(4x – 3)(3x – 2) = 0 (Note: –1 ≠ 0)
ZPP: 4x – 3 = 0 or 3x – 2 = 0
Solve for x: x = ¾ or x =

6. Solve for x: x(x – 2) = –1
Make one side equal zero: x(x – 2) + 1 = 0
Distribute : x2 – 2x + 1 = 0
Factor: (x – 1)² = 0 (Note: This is a ‘special’ polynomial.)
ZPP: x – 1 = 0 (Note: No need to write x – 1 = 0 twice.)
Solve for x: x = 1

Solving Other Polynomial Equations
Solving other polynomial equations is done just like the quadratic equations: Set one side
of the equation to zero, factor, use the zero-product property, and solve for x.

Examples:
1. Solve 4x³ + 16x² + 15x = 0.
This polynomial is already equal to zero, so all we need do is factor, use the ZPP,
and solve for x.

4x³ + 16x² + 15x = 0
Factor: x(2x + 5)(2x + 3) = 0
ZPP: x = 0 or 2x + 5 = 0 or 2x + 3 = 0
Solve for x: x = 0 or x = -5/2 or x = -3/2

2. Solve x3 = 2x² + 99.
Get LHS equal to zero: x3 – 2x² – 99 = 0
Factor: x(x – 11)(x + 9) = 0
ZPP: x = 0 or x – 11 = 0 or x + 9 = 0
Solve for x: x = 0 or x = 11 or x = –9

3. Solve 7x³ – 14x² = 0.
Set one side equal to zero: Already done.
Factor: 7x²(x – 2) = 0
ZPP: 7x² = 0 or x – 2 = 0
Solve for x: x = 0 or x = 2

4. Solve x³ + 18 = 2x² + 9x by factoring.
Set one side equal to zero: x³ + 18 – 2x² – 9x = 0
Rewrite: x³ – 2x² – 9x + 18 = 0
Factor: (xa² – 9)(x – 2) = 0
(x + 3)(x – 3)(x – 2) = 0
ZPP: x + 3 = 0 or x – 3 = 0 or x – 2 = 0
Solve for x: x = –3 or x = 3 or x = 2

5. Solve 30x³ – 3x² – 9x = 0.
Set one side equal to zero: Already done.
Factor: 3x(5x – 3)(2x + 1) = 0
ZPP: 3x = 0 or 5x – 3 = 0 or 2x + 1 = 0
Solve for x: x = 0 or x = 3/5 or x = -½

6. Solve 2(x – 1)² = 2x(x² – 20) + (8x² + 2).
Set one side equal to zero: 2(x – 1)² – 2x(x² – 20) – (8x² + 2) = 0
Simplify : 2(x² – 2x + 1) – 2x(x² – 20) – (8x² + 2) = 0
2x² – 4x + 2 – 2x³ + 40x – 8x² – 2 = 0
Rewrite: –2x³ – 6x² + 36x = 0
Factor: –2x(x + 6)(x – 3) = 0
ZPP: –2x = 0 or x + 6 = 0 or x – 3 = 0
Solve for x: x = 0 or x = –6 or x = 3

Finding x-Intercepts
Finding the x- intercepts of any polynomial is like finding the x-intercepts of a line: set
the equation equal to zero and solve for x. To find the y-intercept, plug zero into the
given formula everywhere an x appears and simplify.

Examples:
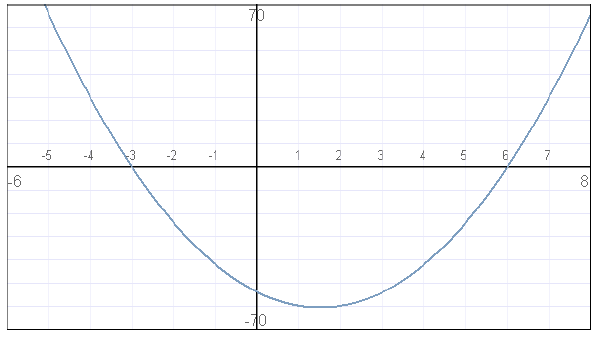
1. Find the x- and y-intercepts of the parabola f (x) = 3x² – 9x + 54
To find the y-intercept, find f(0): (0)² – 9(0) + 54 = 54
To find the x-intercept(s), solve 3x² – 9x + 54 = 0:
Factor: 3(x + 3)(x – 6) = 0
ZPP: x + 3 = 0 or x – 2 = 0 (Note: 3 ≠ 0)
Solve for x: x = –3 or x = 2
Intercepts: (0, 54), (–3, 0), and (6, 0)

The graph of this function looks like the following. Note the x- and y-intercepts
match what was calculated .

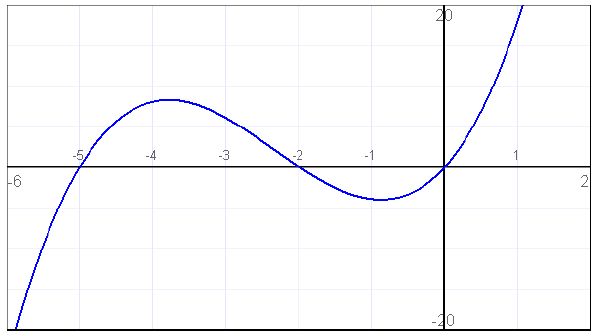
2. Find the intercepts of the graph of the polynomial P(x) = x³ + 7x² + 10x.
To find the y-intercept, find P(0): (0)³ + 7(0)² + 10(0) = 0.
To find the x-intercept(s), set P(x) = 0 and solve for x:
x³ + 7x² + 10x = 0
Factor: x(x + 2)(x + 5) = 0
ZPP: x = 0 or x + 2 = 0 or x + 5 = 0
Solve for x: x = 0 or x = –2 or x = –5
Intercepts: (0, 0), (–2, 0), and (–5, 0)

The graph of this function looks like the following. Note the x- and y-intercepts
match what was calculated.

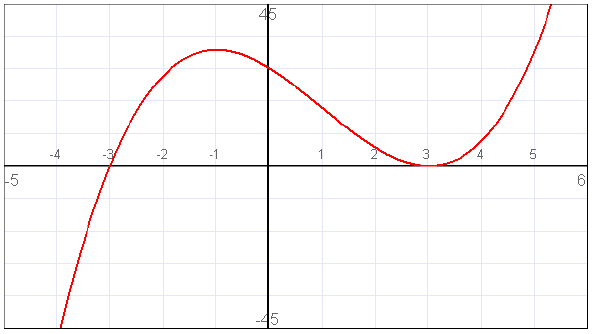
3. Find the x- and y-intercepts of the function f(x) = x³ – 3x² – 9x + 27.
For the y-intercept, find f(0): (0)³ – 3(0)² – 9(0) + 27 = 27.
For the x-intercept(s), set f(x) = 0 and solve for x:
x³ – 3x² – 9x + 27 = 0
Factor: (x + 3)(x – 3)² = 0
ZPP: x + 3 = 0 or x – 3 = 0
Solve for x: x = –3 or x = 3
Intercepts: (0, 27), (–3, 0), and (3, 0)

The graph of this function looks like the following. Note the x- and y-intercepts
match what was calculated.

Solve the following equations by factoring.
1. 3x² – 5x + 2 = 0
2. x³ – x = 0
3. x⁴ + 6x³ + 8x² = 0
4. 3x² + 2x = 8
5. 8x² + 10x = 3
6. 3x² = 2x + 8
7. –42x³ – 148x² – 96x = 0
8. 8x⁴ = 32x²
9. 4x² + 40 = 44x

Find the x- and y-intercepts of the following polynomial functions.
10. f(x) = 7x³ + 21x² – 7x – 21
11. f(x) = 6x² + 7x – 20
12. f(x) = 48x³ + 212x² + 224x
13. P(x) = –4x² + 14x² – 12x
14. P(x) = 7(x – 2)² – 28
15. P(x) = (x – 3)(x – 2)(x + 4)