Subspace Expansion

Abstract—We consider iterative subspace Wiener filters for
solving minimum mean-squared error and minimum variance
unbiased estimation problems in low-dimensional subspaces.
In this class of subspace filters, the conjugate direction and
multistage Wiener filters comprise two large subclasses, and
within these the conjugate gradient and orthogonal multistage
Wiener filters are the most prominent. We establish very general
equivalences between conjugate direction and multistage Wiener
filters, wherein the direction vectors of a conjugate direction filter
and the stagewise vectors of a multistage filter are related through
a one- term autoregressive recursion. By virtue of this recursion,
the expanding subspaces of the two filters are identical, even
though their bases for them are different . As a consequence, their
subspace filters, gradients, and mean-squared errors are identical
at each stage of the subspace iteration. If the conjugate direction
filter is a conjugate gradient filter, then the equivalent stagewise
filter is an orthogonal multistage filter, and vice-versa. If either
the conjugate gradient filter or the orthogonal multistage filter is
initialized at the cross-covariance vector between the signal and
the measurement , then each of the subspace filters iteratively
turns out a basis for a Krylov subspace.

Index Terms—Keywords: minimum mean-squared error filters,
Wiener filters, conjugate direction filters, conjugate gradient
filters, multistage filters, orthogonal multistage filters, quadratic
minimization, Krylov subspace.

I. INTRODUCTION

Rank- reduction is now an important element of many signal
processing algorithms that aim to reduce the dimension of
a measurement space in advance of detection, estimation,
classification, beamforming, or spectrum analysis. The idea,
in the analysis stage, is to linearly resolve a measurement
onto a sequence of expanding subspaces, until a satisfactory
trade-off has been achieved between the increased bias and
reduced variance associated with rank reduction. If the linearly
resolved measurements have a simple correlation structure
then the implementation of the reduced dimension filter in
the synthesis stage will be efficient.

This paper is addressed to iterative subspace Wiener filters
for solving minimum mean-squared error and minimum
variance unbiased estimation problems in low-dimensional
subspaces. In this class of subspace filters, the conjugate
direction and multistage Wiener filters comprise two large subclasses,
and within these the conjugate gradient and orthogonal
multistage Wiener filters are the most prominent.

The conjugate gradient algorithm for iteratively solving
quadratic minimization problems was discovered by Hestenes
and Stiefel in 1952 [1], and the multistage Wiener filter was
discovered by Goldstein and Reed in 1998 [2]. In spite of
the fact that there is no essential difference between quadratic
minimization, the solving of linear systems, and Wiener filtering,
the connection between conjugate gradient algorithms
and multistage filtering was not made until Dietl et al. [8],
and Weippert and Goldstein [3], [4], recognized a connection
between conjugate gradients and orthogonal multistage Wiener
filters. This insight was based on work by Honig, Xiao, Joham,
Sun, Zoltowski, and Goldstein, subsequently published in [5],
[6], [7], [8], regarding the Krylov subspace underlying the
multistage Wiener filter. Further connections were reported by
Zoltowski in his 2002 tutorial [9].

Our first aim in this paper is to further refine what is
currently known about connections between conjugate gradient
and multistage Wiener filters, by appealing to fundamental
insights in least -squares filtering. In so doing we clarify the
sense in which conjugate gradient and multistage filters are
compelling, rather than ad hoc, realizations of iterative filters.

Our second aim is to enlarge our understanding of iterative
subspace filtering by showing that there is an even larger class
of equivalences, of which the equivalence between conjugate
gradients and orthogonal multistage Wiener filters is only
a special case. That is, for every conjugate direction filter
there is an infinite family of equivalent multistage filters and,
conversely, for every multistage filter there is an infinite family
of equivalent conjugate direction filters. The fact that a multistage
Wiener filter has a conjugate direction implementation,
or vice-versa, is just a consequence of the autoregressive
connection between stagewise filters and conjugate directions.
If the stagewise filters are orthogonal, and they are initialized
at the cross-covariance vector between the signal and
the measurement, then they are an orthogonal basis for a
Krylov subspace. The equivalent conjugate direction filter is
then a conjugate gradient filter whose direction vectors are a
nonorthogonal (but conjugate with respect to the covariance
matrix) basis for the same Krylov subspace. Conversely, if the

conjugate direction filter is a conjugate gradient filter, then
its equivalent multistage filter is orthogonal. Both turn out a
basis for the same Krylov subspace, assuming the conjugate
gradient filter is initialized at the cross-covariance.
It is worth emphasizing that our arguments are based
entirely on the algebraic structure of iterative subspace Wiener
filters, with no appeal to specific algorithms for computing
conjugate direction or multistage vectors. Late in the paper,
conjugate gradients are used only to illustrate general principals.

II. FILTERING AND QUADRATIC MINIMIZATION

Let us define the problem of linear minimum mean-squared
error estimation as follows. The complex scalar 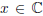is a
random variable to be estimated from the complex vector of
measurements, 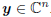. We shall assume that the signal x and
measurement y share the composite covariance matrix

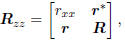
where 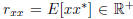is the scalar variance of x, r =
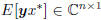is the vector covariance of (x, y), and R =
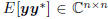is the matrix covariance of y. Throughout,
we use superscript  * to denote Hermitian transpose.
From this second-order description we may write the meansquared
error of estimating x from w y as

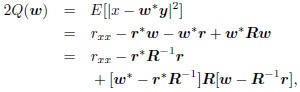
with minimum value 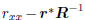at the Wiener solution w
satisfying Rw = r. This is a consequence of the principle of
orthogonality, which says .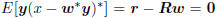
This is the way a filtering theorist describes the filtering
experiment. An optimization theorist would say the problem
is to minimize the quadratic function Q(w), whose gradient
is 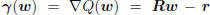, and whose Hessian is
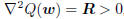, meaning the minimum is achieved where
the gradient is 0, namely 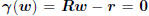. So a zero
gradient plays the same role in optimization theory as the
principle of orthogonality plays in filtering theory.

III. THE ALGEBRA AND GEOMETRY OF ITERATIVE
SUBSPACE WIENER FILTERS

Let us frame our discussion of iterative subspace Wiener
filters as follows. The complex scalar 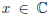is a random
variable to be estimated from the complex vector of measurements,
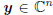. These measurements are a basis for the
Hilbert subspace 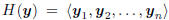, and any linear
estimate of x will lie in this subspace. Let us suppose that
we approach the filtering or optimization problem by first
resolving the measurements onto a k-dimensional basis A_k =
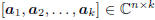to produce the vector of coordinate
values
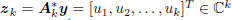. In this notation,
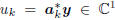is the kth complex scalar coordinate of

y, in the coordinate system A _k. The trick is to determine
a simple algorithm for expanding this subspace in such a way
that H(z_k) is near to H(y) and the covariance matrix of z_k
is easy to invert.

The variables (x, z_k) share the composite covariance matrix

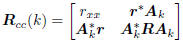
From this second-order description of the composite vector
we may write the mean-squared error of estimating x from
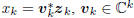, as

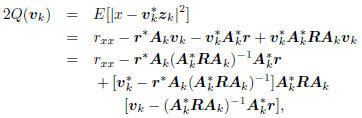
with minimum value 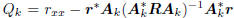at
the kth Wiener solution vk satisfying .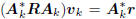
This is a consequence of the principle of orthogonality, which
says 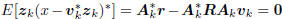. But w_k =
A_kv_k is just the kth approximation to the Wiener filter w =
R^-1r. Thus, this orthogonality condition may also be written
as

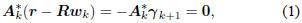
where 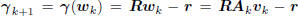is the
gradient of Q(w_k). This orthogonality may be iterated to
derive the important result that



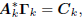
where 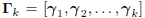is the matrix of gradients, and
C_k is a lower triangular matrix.

The importance of this formula is the following : no matter
how the coordinate system A_k is chosen, its basis will be
orthogonal to the current gradient 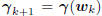at w_k =
A_kv_k, and all future gradients. Thus, as long as the current
gradient is non-zero, the subspace 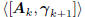will continue
to expand in dimension, as a direct sum of the subspaces
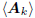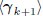and . Thus, there is a clear suggestion that as
new coordinates of the form 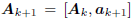are built,
the old coordinates A_k and the gradient 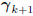are compelling
candidates in this expansion.

To this point we have required nothing special about the
coordinate system A_k and its corresponding analysis filters
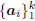. Moreover, even though gradient expansion looks compelling,
there is, as yet, no indication of how these filters
might be iteratively computed. Nonetheless, as the following
arguments show, there is quite a lot that may be said about
the geometry of the approximating Wiener filters w_k = A_kv_k
and estimators 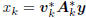. This geometry is inherited from
the gradient orthogonality 
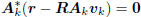in (1).

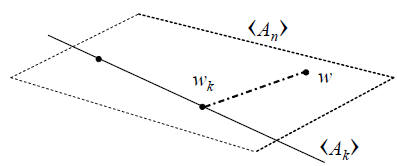
Fig. 1. Geometry of interative approximation to the Wiener filter.

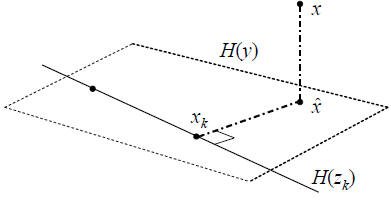
Fig. 2. Geometry of interative approximation to the Wiener solution.

A. Geometry of Filters and Estimators
Consider the inner product

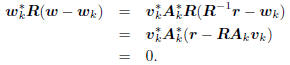
Thus, as illustrated in Figure 1, w_k orthogonally decomposes
w = R^-1r as w = w_k +(w−w_k) with respect to the norm
w*Rw.
There is a related story to be told for the sequence of
estimators 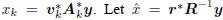, and consider
the inner product

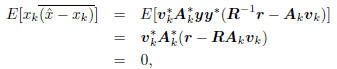
where the overline notation denotes complex conjugation.
Thus, as illustrated in Figure 2, x_k orthogonally decomposes
.

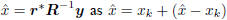These results show that subspace expansion to 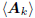for
purposes of approximating w and x by wk and x_k may
as well be viewed as subspace (or rank) reduction. These
conclusions are still general, requiring nothing special, like
conjugate directions, for the analysis filters A_k.

B. The Krylov Subspace
If A_k is a basis for the Krylov subspace 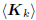, where
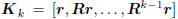is the Krylov matrix of Krylov
vectors, then 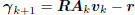is a linear combination of

the Krylov vectors 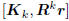, and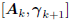 is a basis for
the Krylov subspace 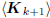. By choosing v_o = 0, in which
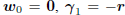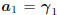case , and , then A₁ = −r and
the induction argument is initialized. Moreover, the basis
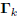
will be an orthogonal basis for the Krylov subspace .
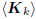What makes this argument go is the fact that w_k = A_kv_k is
computed from the optimum Wiener filter v_k in the coordinate
system A_k.

Thus, every subspace Wiener filter that is initialized at the
one-dimensional subspace <r> and expanded using a linear
combination of the current subspace and current gradient,
will turn out an orthogonal basis for the Krylov subspace.
This conclusion has nothing whatsoever to do with the actual
algorithm used. Thus, this Krylov property is not peculiar to
any particular algorithm for designing subspace Wiener filters.

IV. ALGEBRAIC EQUIVALENCES

When we talk about a conjugate direction filter, then we
say the analysis stage consists of the direction vectors A_k=
D_k = [d₁, d₂, . . . , d_k] where 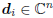. A conjugate direction
Wiener filter is an iterative subspace Wiener filter in which the
coordinates of the original measurement in the direction subspace
are uncorrelated. That is, 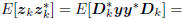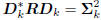, where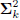
is diagonal. We say the directions
are R-conjugate. The resulting iterative Wiener filter may then
be synthesized in a forward synthesis, and error formulas are
continued sums, a fact that is obvious, but not derived in this
paper.

When we talk about a multistage filter we say the analysis
stage consists of the multistage vectors A_k = G_k =
[g₁, g₂, . . . , g_k], where 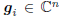. A multistage Wiener filter
is an iterative subspace Wiener filter in which the coordinates
of the original measurement in the multistage subspace are
tridiagonally correlated. That is,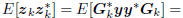
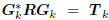
, where T_k is tridiagonal. The resulting
iterative Wiener filter may then be synthesized in a backward
synthesis, and error formulas are continued fractions , a fact
that is almost obvious, but not derived in this paper.

Our aim is to show that for every conjugate direction Wiener
filter there is a family of equivalent multistage Wiener filters,
and vice-versa. Because of the autoregressive recursion that
will connect the conjugate direction vectors to the stagewise
vectors, the two implementations will share a common expanding
subspace. Thus Wiener filters will be computed in
a common subspace, and neither can outperform the other.

Generally the underlying subspace is not Krylov, so the
motivation to design something other than a standard conjugate
gradient or orthogonal multistage filter would be to construct
an expanding subspace that is better matched, for k < n, to
the optimum Wiener filter than is the Krylov space. If the
conjugate direction filter is a conjugate gradient Wiener filter,

and its corresponding multistage Wiener filter is orthogonal,
then both are stuck in the Krylov subspace.

A. Conjugate direction and multistage Wiener filters
The idea behind any conjugate direction algorithm is to
force the coordinates z_k to be uncorrelated. That is,

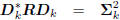: diagonal,
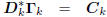: lower triangular,

where 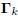is the matrix of gradients and C_k is a lower
triangular matrix. Now suppose the filters G_k are defined
according to a first-order autoregressive recursion =
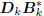G_k, for some arbitrary upper bidiagonal 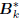. These filters
define the multistage Wiener filter

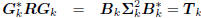: tridiagonal,
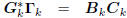: lower triangular.

The arbitrary choice of lower bidiagonal B_k indicates that
there are infinitely many multistage Wiener filters that are
equivalent to the given conjugate direction algorithm.

Conversely, suppose we start with a multistage Wiener filter

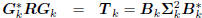: tridiagonal,
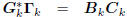: lower triangular,

where 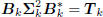is a lower-bidiagonal–diagonal–upperbidiagonal
factorization of the tridiagonal matrix T_k. Define
the filters D_k according to the first-order autoregressive recursion
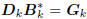. These filters define a conjugate direction
Wiener filter

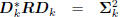: diagonal,
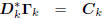: lower triangular.

The arbitrary scaling of B_k and 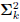in the factorization
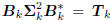means there is an infinite family of conjugate
direction Wiener filters that are equivalent to a given
multistage Wiener filter.

In summary, for every conjugate direction Wiener filter
there is a family of equivalent multistage Wiener filter, and
vice-versa. They share common filters, gradients, and meansquared
errors, but nothing special may be said about these
gradients or subspaces, except that they are common.

B. Conjugate gradient and orthogonal multistage Wiener filters

A conjugate direction algorithm is called a conjugate gradient
algorithm if the current direction vector is a linear
combination of the current negative gradient and the previous
direction vector [10]. In this case, the direction vectors D_k
are computed according to the conjugate gradient algorithm
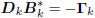, where 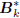is an upper bidiagonal matrix, the
resulting gradients are orthogonal, and they tridiagonalize R:

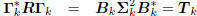: tridiagonal,
: diagonal.

The orthogonality of the gradient matrix 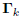follows from
the fact that B_k and 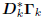are lower triangular, as is their
product, and the only Hermitian lower triangular matrix is
diagonal. We may follow the argument of [11] to show that
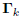is an orthogonal basis for the Krylov subspace .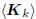

In summary, any conjugate gradient Wiener filter defines
an equivalent orthogonal multistage Wiener filter whose filters
are G_k = −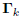, whose gradients are 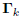, and whose meansquared
error is the same as for the conjugate gradient

Wiener filter. Both filters turn out a basis for the Krylov
subspace 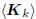, provided the conjugate gradient Wiener filter
is initialized at the cross-covariance r.

Conversely, suppose we start with an orthogonal multistage
Wiener filter
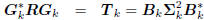: tridiagonal,
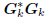: diagonal,
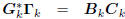: lower triangular.

and define the direction vectors 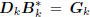. Then these
directions define a conjugate direction algorithm:

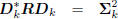: diagonal,
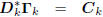: lower triangular.

Both G_k and 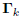are a causal basis for 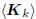, meaning that
G_k= 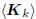U_k, where U_kis upper triangular. Thus,
diagonal: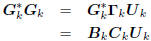: lower-times-upper.
We deduce from this that the upper triangular U_kand the
lower triangular B_kC_kare in fact diagonal. This means
G_k = 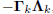, where k is diagonal, and .
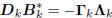Thus the conjugate direction algorithm is a conjugate gradient
algorithm.

In summary, any orthogonal multistage Wiener filter determines
an equivalent conjugate gradient Wiener filter whose
filters, gradients, and mean-squared errors are the same as
for the orthogonal Wiener filter. The gradients are within a
diagonal matrix of the orthogonal multistage vectors (i.e., each
multistage vector is a scaled gradient). Both filters turn out a
basis for the Krylov subspace 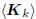, provided the orthogonal
multistage Wiener filter is initialized at the cross-covariance
r.

C. Further Observations
All subspace expanding filters of the form 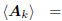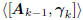have the property that

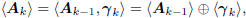
where the orthogonality comes from (1). If the A_k are composed
of conjugate directions, and A₁ = [a₁] with a₁ = r,
then the A_k diagonalize R and build out a nonorthogonal basis
for the Krylov subspace. Moreover, the 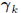tridiagonalize R.
The A_k (and 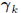) may be generated by any conjugate direction
algorithm or any corresponding multistage Wiener filter.

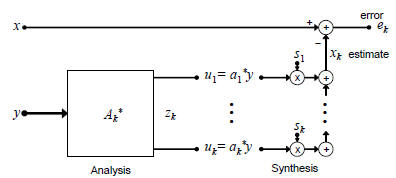
Fig. 3. Analysis and synthesis filters in a subspace expanding filter.

V. MORE ON THE ALGEBRA AND GEOMETRY OF
CONJUGATE GRADIENT AND ORTHOGONAL MULTISTAGE
WIENER FILTERS

We have established the algebraic equivalence of conjugate
direction and multi-stage Wiener filters, thereby establishing
that their solutions and performances are equal at each iteration
(or stage) k. This generalizes prior results [3], [4] that
established the equivalence between conjugate gradient and
orthogonal multistage filters.

But what about the geometry of algorithms for expanding
the Krylov subspace in the conjugate gradient and multistage
filters? In this section we give the well-known conjugate gradient
algorithm, establish its action on the composite covariance
matrix R_cc, and illustrate the geometry of subspace expansion
for approximating the Wiener filter w and its error x −w*y.

Let us begin with Figure 3, and analyze the action of the
analysis stage 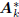on the covariance matrix R_cc:

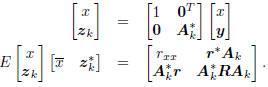
If the analysis filters A_k are conjugate direction, then the k×k
matrix A
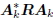in the south-east block above is diagonal:


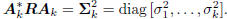
Now, with 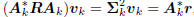, take the composite
vector (x, z_k) to its error form, as in Figure 3 with v_k =
[s₁, . . . , s_k]^T :

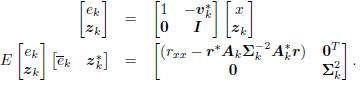
These equations hold for any subspace expansion in which
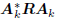= diag 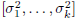, meaning z_k is a white vector.
This is characteristic of all conjugate direction algorithms.
Of all algorithms for producing conjugate directions, the
most famous is the conjugate gradient algorithm [1]:
Initialize: .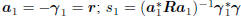
For k = 2, 3, . . . until convergence (k≤n) do
Compute gradient: ;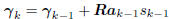
Compute direction:

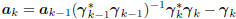
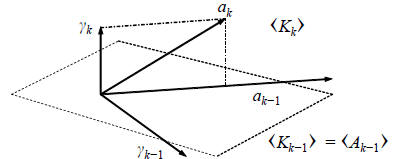
Fig. 4. Geometry of subspace expansion in the conjugate gradient Wiener
filter.

Compute step size: .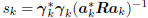

The corresponding filters and estimators at each iteration (or
stage) are v_k = [s₁, . . . , s_k]^T , w_k = w_k-1 +a_ks_k, and x_k =
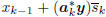, with w₁ = a₁s₁ and x₁ = 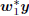. Thus all
recursions are forward recursions, with no recomputation of
steps, filters, or estimates as stages are added.

The geometry of this expansion is illustrated in Figure 4.
The first important insight is that the new direction vector a_k
is an autoregressive recursion on the old: a_k = ka_k-1 − k.
This is just the simplest of recursions on {a₁, . . . , a_k-1} that
would have produced the same conjugate direction effect. The
second insight is that the Krylov subspace 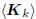expands as
the direct sum 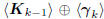, further justifying the term
conjugate gradient. Of course, if the A_k are composed of
conjugate directions, and A₁= [a₁] with a₁ = r, then a
gradient subspace expansion may be realized with a conjugate
gradient algorithm or its corresponding orthogonal multistage
Wiener filter.

VI. CONCLUSIONS

Our conclusions are the following:
• For any iterative subspace Wiener filter, the subspace A_k
of dimension k is orthogonal to the current and future
gradients 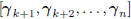. This is the orthogonality
principle at work.
• Iterative subspace Wiener filters and their corresponding
estimators orthogonally decompose full-rank solutions,
making them (equivalently) dimension-expanding
or dimension-reducing solutions.
• Any subspace expansion in an iterative subspace Wiener
filter that uses the direct sum of the past subspace and
the current gradient turns out an orthogonal basis for the
Krylov subspace, assuming the algorithm is initialized at
the cross-covariance vector.
• For every multistage Wiener filter there is a family of
equivalent conjugate direction Wiener filters, with identical
subspaces, gradients, and mean-squared errors. And
vice-versa.
• For every orthogonal multistage Wiener filter there is a
family of equivalent conjugate gradient Wiener filters,
with identical subspaces, gradients, and mean-squared
errors. And vice-versa.
• If an orthogonal multistage Wiener filter is initialized at
the cross-covariance, then it and its equivalent conjugate

gradient Wiener filter turn out the Krylov subspace. And
vice-versa.
Acknowledgment. The authors acknowledge insightful discussions
with L. Todd McWhorter in the early stages (k =
1, 2) of this work.

REFERENCES

[1] M. R. Hestenes and E. Stiefel, “Methods of conjugate gradients for
solving linear systems,” J. Res. Nat. Bur. Stand., vol. 49, pp. 409–436,
1952.
[2] J. S. Goldstein, I. S. Reed, and L. L. Scharf, “A multistage representation
of the Wiener filter based on orthogonal projections,” IEEE Trans.
Inform. Th., vol. 44, no. 7, pp. 2943–2959, Nov. 1998.
[3] M. E.Weippert and J. S. Goldstein, “Relationship between the multistage
Wiener filter and the method of conjugate gradients,” Internal SAIC
Memorandum, August 31, 2001 (Patent pending).
[4] M. E. Weippert, J. D. Hiemstra, J. S. Goldstein, and M. D. Zoltowski,
“Insights from the relationship between the multistage Wiener filter and
the method of conjugate gradients,” Proc. IEEE Workshop on Sensor
Array and Multichannel Signal Processing, 4–6 August, 2002.
[5] M. D. Zoltowski and J. S. Goldstein, “Reduced-rank adaptive filtering
and applications,” Tutorial, ICASSP 2001, Salt Lake City, May 2001.
[6] M. L. Honig and W. Xiao, “Performance of reduced-rank linear interference
suppression,” IEEE Trans. Inform. Th., vol. 47, pp. 1928–1946,
July 2001.
[7] M. Joham, Y. Sun, M. D. Zoltowski, M. L. Honig and J. S. Goldstein,
“A new backward recursion for the multistage nested Wiener filter
employing Krylov subspace methods,” Proc. IEEE MILCOM, October
2001.
[8] G. Dietl, M. D. Zoltowski, and M. Joham, “Recursive reducedrank
adaptive equalization for wireless communications,” Proc. SPIE,
vol. 4395, April 2001.
[9] M. D. Zoltowski, “Conjugate gradient adaptive filtering with application
to space-time processing for wireless digital communications ,” Plenary
Lecture Viewgraphs, published in Proc. IEEE Workshop on Sensor Array
and Multichannel Signal Processing, 4–6 August, 2002.
[10] E. K. P. Chong and S. H. ˙ Zak, An Introduction to Optimization, Second
Edition. John Wiley and Sons, Inc., New York, NY, 2001.
[11] G. H. Golub and C. F. Van Loan, Matrix Computations. The Johns
Hopkins University Press , Baltimore, MD, 1983, p. 324.