Given two sets X and Y , a function is a rule that associates each member
of X with
exactly one member of Y . That is, some x goes in, and some y comes out. These
notations are used to describe functions:
f : X →Y
y = f (x)
In these cases, x is called the independent variable and y the
dependent
variable. That is, we can pick any value of x we want to stick into the
function, but
we can’t really pick what value y takes on—that depends on x.
When f is a function from X into Y , the set X is called the domain of
the function
and Y is called the range. The domain is the set of permissible values to
stick into
the function, and the value that the function takes must be somewhere within the
range. Most functions used are real-valued functions: functions whose domains
and ranges are the set of real numbers or some subset thereof. We use the letter
R
to denote real numbers, and we write a real-valued function as f :R→R.
(You put
a real number in, and you get a real number out.)
In economics, the amount of a good x demanded is a function of the price of that
good. In other words,
x = x(p)
This is called a demand function. Sometimes the same letter will be used
to
denote the function as the dependent variable .
Functions are sometimes referred to as mappings. Really, functions are
only a
specific type of mappings: those in which the output is a single element.
Sometimes
we want to divide functions into several types:
One-to-one (injective): Each member of the range comes from at most
one element in the domain. (There are not two xes that give the same y.)
Many-to-one: There are multiple xes that give the same value of y.
Onto (surjective): Each member of the range gets used at least once.
One-to-one and onto (bijective): Each member of the range gets used
exactly once (by exactly one x value).
Example: The function is f (x) = x , with the domain given as (−∞,∞) and
the range
also as (−∞,∞) . This is a one-to-one mapping, since there are not two x values
that give you
the same f (x) . It is also onto, since each y between −∞ and +∞ gets used.
Therefore, it is a
bijective mapping.
Example: The function is f (x) = x2 ,
with the domain given as (−∞,∞) and the range
also as (−∞,∞) . This is not a one-to-one mapping, since there are multiple x
values that give
you the same f (x) ; for example, f (-2) = 4 = f (2) . Nor is it onto, since
negative values of y
are never given (there is no value of x that gives you f (x) = -12 , at least
not among real
numbers—which is what we defined the domain as). Therefore, it is simply a
many -to-one
function.
Example: The function is f (x) = x2 , with the domain given as
[0,+∞) and the range
also as [0,+∞) . This is a one-to-one mapping, since there are not multiple x
values that give
you the same f (x) . It is also onto, since all numbers in the range of y are
used by some x value.
Since it is both one-to-one and onto, it is bijective.
The moral: whether a function is injective, surjective, both, or neither depends
on
the function, the domain, and the range together. We are most likely to care
about
whether a function is bijective, since this means that the function is
invertible. If
f : X →Y is invertible, this means that there exists another function f -1
:Y → X
such that:
y = f (x) is equivalent to : x = f -1 (y) .
Even if you don’t remember the vocabulary, keep in mind that these two
conditions
are necessary to guarantee that the inverse of a function is itself a function.
The demand function tells us how much a person wants to buy at a certain price.
If a
business knows this, it might ask the question, “given that I would like to get
people
to buy x units, what price should I charge?” The business would simply find what
is
called the inverse demand function:
x = x( p) is equivalent to: p = x -1 (x( p)) = p(x) .
However, this is only solvable provided the demand function meets the two
requirements given above. Does it, though?
Some functions go up and down and all over the place. A fairly boring function
doesn’t, and we call these boring functions monotonic. Here are those
definitions:
|
(Weakly) increasing: |
 |
|
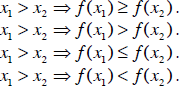Strictly increasing: |
|
(Weakly) decreasing: |
|
Strictly decreasing: |
|
(Weakly) monotonic: |
Either weakly increasing or weakly decreasing. |
|
Strictly monotonic: |
Either strictly increasing or strictly decreasing. |
Example: The function is f (x) = x , with domain of
(−∞,∞) and range of (−∞,∞) .
This is a strictly increasing function, since a larger value of x means a larger
value of f (x) . (Of
course, you can also call it weakly increasing — technically it satisfies this
definition, though it’s
a bit silly to mention “weakly” when we know it is strictly—and it is also
strictly monotonic.)
This makes it invertible, and f -1(y) = y .
Example: The function is f (x) = x , with domain of (−∞,∞) and range of
(−∞,∞) .
This is not a monotonic function, since it sometimes it decreases and sometimes
it increases. The
function is not invertible.
Example: The function is f (x) = x , with domain of [0,+∞) and range of
[0,+∞) . On
this domain, the function is strictly increasing, so it is also strictly
monotonic. This function is
invertible, and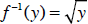 
. (On the last example, it
would be wrong to say that an inverse of
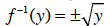exists, since a function can take on only
one value. A “correspondence” is a type
of mapping that can, but we won’t meet those until later in the course.)
Example: The function is f (x) = x , with domain of (−∞,∞) and range of
(−∞,∞) .
This function satisfies the definition of (weakly) increasing and (weakly)
decreasing, so it is also
(weakly) monotonic. However, since it is not strictly monotonic, no inverse
exists.
Back to the demand curve : provided that x = p(x) is strictly monotonic, an
inverse
demand function exists.
Another important property of functions is continuity. A continuous function is
one
that can be drawn with a single , continuous brushstroke. Technically, a function
f is
continuous at a point x if for any ε > 0 there exists a
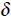> 0 such that if a point y is
less than distance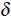 
from x, then f (y)
- f (x) is less ε . The function is
continuous
if it is continuous at every point in its domain.
Less stringent than continuity is piecewise continuity. This describes a
function
that has only a finite number of points of discontinuity within any finite
interval.
At a point where a function is continuous, you can take a derivative to see how
the
value of f (x) changes when x changes . The derivative of f at a point x
is:
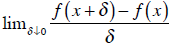
The derivative of f might be denoted by f ' (x) or, when y
= f (x) , by dy /dx . The
function is continuously differentiable at a point x when its derivative
is a
continuous function at that point. When it is continuously differentiable at all
points, it is called a continuously differentiable function.
Sometimes you will see the notation f ∈C or f ∈CX (where X is the
domain of f) to
indicate that f is a continuous function. C is the set of continuous functions.
If f is
continuously differentiable, this is written f ∈C1 . If it is
twice continuously
differentiable, f ∈C2 , and so forth for higher-order
derivatives. Being twice
continuously differentiable implies being (once) continuously differentiable,
which in
turn implies being continuous.
