This is a more complete version posted later on Monday.
I'm not planning
to attach exercises; I may eventually complete the construction of the general
reals if I can see the least tangled way to do it!
We begin our construction with the system of positive
rational numbers ,
supposed already understood.
Axioms which are true in the positive rationals and in the
reals:
Commutative laws: Addition and multiplication are
commutative operations.
Associative laws: Addition and multiplication are
associative operations.
Distributive law : x(y + z) = xy + xz as usual.
Identity for multiplication: 1 is the identity
element for multiplication.
Inverse law for multiplication : Every number a has
a multiplicative inverse
a-1. (recall that zero is not in our system).
Definition: We define x < y as
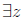(x + z = y) then >, ≤, ≥ are defined
using < as usual.
Trichotomy 1: For any x and y, either x < y, y < x, or x = y.
Trichotomy 2: For any x and y, either
¬x < y or ¬y < x.
The usual properties of order in this context are fairly easy to prove from
these axioms. We give some properties which may not be entirely obvious.
transitivity: If x < y and y < z then there are u; v such that x+u = y and
y + v = z, so (x + u) + v = z, so x + (u + v) = z, so x < z.
additive cancellation : If a + c = b + c then a = b: suppose a + c = b + c
and a ≠ b. Then either a < b or b < a; suppose the former without loss
of generality. We have k such that a+k = b. Then a+c = (a+k)+c,
whence a + c = (a + c) + k, whence a + c < a + c, which is ruled out
by Trichotomy 2.
monotonicity of addition: If a < b then there is k such that a + k = b,
whence (a +c)+k = (a +k)+c = b+ c so a +c < b +c. On the other
hand, if a + c < b + c then there is k such that (a + c) + k = b + c,
whence (a + k) + c = b + c, whence a + k = b by additive cancellation ,
so a < b.
monotonicity of multiplication: If a < b then there is k such that a+k =
b, whence ac + kc = (a + k)c = bc, so ac < bc. On the other hand,
if ac < bc it follows that there is k such that ac + k = bc, whence
(ac + k)c-1 = bcc-1, whence a + kc-1 = b, so a < b.
The positive reals satisfy the Least Upper Bound Property in addition to
these axioms.
We need one more property of the positive rationals to make our proofs
work (related to the induction property of the natural numbers):
Induction Property: For any positive rational x, any nonempty set of positive
rationals which is downward closed and closed under addition of
x contains all positive rationals.
This can be understood as keeping in nitesimal quantities out of our
system.
A corollary of this axiom which we also use is the following:
Unbounded Powers : For any x > 1, any nonempty set of positive rationals
which is downward closed and closed under multiplication by x contains
all positive rationals.
Proof: Let x > 1. Then x = 1 + e for some e. Let I be a nonempty
set of positive rationals which is downward closed and closed under
multiplication by 1 + e. Let a be an element of this set. Now we show
that I is nonempty and closed under addition of ea: for any y ∈ I, we
know that y(1 + e) ∈ I. If y ≤ a then y + ea ≤ a + ea = a(1 + e)
∈ I.
If y > a, then y + ea < y + ey = y(1 + e) ∈ I.
With any positive real r a unique set Lr is associated: the set of all
positive rationals q < r.
Definition: A set A is said to be a Dedekind left set if it is a set of positive
rationals (the set of all positive rationals is denoted by
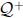) with the
following properties:
1. A ≠ ø ; and A ≠
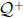
2. A is downward closed: if a is a positive rational, b is a positive
rational, b < a, and a ∈ A, then b ∈ A.
3. A has no largest element.
Observation: The Dedekind left sets are exactly the sets Lr for arbitrary
real numbers r . It is easy to verify that each Lr actually has these
properties, and further that if A is a Dedekind left set, it is equal to
Lr where r is the least upper bound of A.
Now we propose to define the positive real numbers as Dedekind left sets.
Definition: We define a (Dedekind) positive real number as a Dedekind left
set of positive rationals. If R and S are positive real numbers, we de ne
R + S as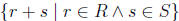 
and R · S as
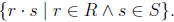
A little attention to notation is required here: a more explicit way to
write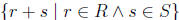 
is 
We need to prove that S + T and S · T are actually Dedekind positive
reals.
Suppose that S and T are Dedekind positive reals. S + T and S
· T
are clearly both nonempty. Suppose s'
s and t'
t. Since s' exceeds all
elements of S and t' exceeds all elements of T, we see that s' + t' exceeds all
elements of S +T and s' · t' exceeds all elements of S · T. Thus neither S +T
nor S · T are the entire set of positive rationals. Now we need to show that
both sets are downward closed. Suppose s ∈ S and t ∈ T and u < s + t.
It is straightforward to show that either
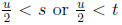(suppose otherwise
and show u ≥ s + t). Suppose without loss of generality that
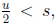so
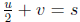for some v. Express u as
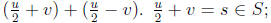since
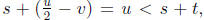we have
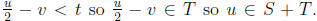
Now suppose that u < st. u = ut-1t < st so ut-1 < s so ut-1
∈ S whence
u ∈S · T. So both S + T and S · T are downward closed. Now if s ∈ S
and t ∈ T, note that if s' > s is an element of S we have s' + t > s + t and
s't > st, so if we are presented with an element of either S + T and S · T we
can produce a larger element of the same set. This completes the argument
for closure of the Dedekind positive reals under the defined addition and
multiplication operations .
We proceed through the veri cation that the Dedekind positive reals have
the expected properties.
Commutative properties:
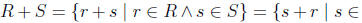
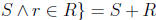by commutativity of addition of positive rationals
(and if one wants to be technical, by commutativity of ^ as well). The
proof for commutativity of multiplication is exactly the same.
Associative properties: We show that x ∈ (R + S) + T if and only if
x ∈ R+(S +T) for any positive rational x and Dedekind positive reals
R; S; T.
Suppose x is any positive rational number and R; S; T are any Dedekind
positive reals.
Suppose that x
∈ R + (S + T). Then there is u ∈ R and v ∈ S + T
such that u + v = x. Further, there is a ∈ S and b ∈ T such that
a + b = v. So u + (a + b) = x, whence (u + a) + b = x. Now observe
that u + a ∈ R + S and b ∈ T, so x ∈ (R + S) + T.
Suppose that x ∈ (R + S) + T. Then there is u ∈ R + S and v ∈ T
such that u + v = x, and, further, there is a ∈ R and b ∈ S such that
a+b = U. So (a+b)+v = x, whence a+(b+v) = x, whence (because
a ∈ R and b + v ∈ S + T) we have x ∈ R + (S + T).
Since (R + S) + T and R + (S + T) have the same elements, they are
the same set.
The proof of associativity of multiplication is exactly analogous.
