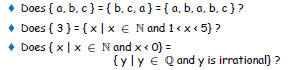• Terminology
• Set: a collection of objects
• Element or Member of a set: an object belonging to the set
• Three ways to designate sets:
• word description
ex: the set of odd counting numbers between 2 and 12
• the listing method
ex: {3, 5, 7, 9, 11}
• set-builder notation
ex: {x | x ∈N, x is odd, and x < 12}
• Notes:
• use curly braces to designate sets,
• use commas to separate set elements
• the variable in the set -builder notation doesn’t have to be x.
• use ellipses (. . . ) to indicate a continuation of a pattern
established before the ellipses
ex: {1, 2, 3, 4, . . . , 100}
• N Natural or Counting numbers: {1, 2, 3, . . . }
• W Whole Numbers: {0, 1, 2, 3, . . . }
• I Integers: {. . . , -3, -2, -1, 0, 1, 2, 3, . . . }
• Q Rational numbers :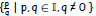 
• 
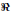- Real Numbers : { x | x is a number that can be written as a
decimal }
• Irrational numbers: { x | x is a real number and x cannot be
written as a quotient of integers }.
Examples are: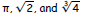 
• 
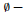Empty Set: { }
Notes
• The symbols { x | x . . . } is read "x such that x . . .
has some
property
• The symbol ∈means is "an element of"
• Any rational number can be written as either a
TERMINATING decimal ( like 0.5, 0.333, or 0.8578966)
or a
REPEATING decimal ( like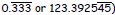 
• The decimal representation of an irrational number never
terminates and never repeats
• The set {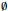 
} is not empty, but is a set which contains the empty
set
Set Cardinality
• Cardinality of a set: the number of distinct elements in
the set
• textbook: n(A) - or we can use |A|
• If the cardinality of a set is a particular whole number, we call
that set a finite set
• If a set is too large to ever finish the counting process, it is called
an infinite set
• Well-Defined set: one for which we can determine
membership,
i.e., given any arbitrary value we can determine conclusively
whether or not that value is in the set
Set Membership
• Well-Defined means that given a set and an object, we
can
determine if the set contains that object
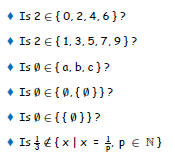
Set Equality
• Set Equality: the sets A and B are equal (written A = B)
provided:
• every element of A is an element of B, and
• every element of B is an element of A
i.e., if they contain exactly the same elements
