Basic Number Theory
Definitions
• Even and Odd numbers
 A number n from Z is called even iff A number n from Z is called even iff
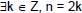 . .
 A number n from Z is called odd iff A number n from Z is called odd iff
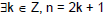 . .
• Prime and Composite numbers
 A number n from Z is called prime
iff A number n from Z is called prime
iff
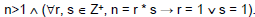
 A number n from Z is called
composite iff A number n from Z is called
composite iff
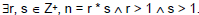 |
Definitions
• A real number r is called rational if
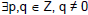 , such that r = p / q. , such that r = p / q.
 Is 0.121212… a rational number? Is 0.121212… a rational number?
 Every rational number can be written
as a repeating or Every rational number can be written
as a repeating or
terminating decimal .
 Every integer is a rational number. Every integer is a rational number.
• All real numbers which are not rational are called irrational. |
• If n and d are both integers, then
n is divisible by d iff 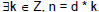 . .
Notation: d | n
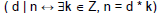
 Synonymous statements: Synonymous statements:
 n is a multiple of d n is a multiple of d
 d is a factor of n d is a factor of n
 d is a divisor of n d is a divisor of n
 d divides n d divides n |
Theorem: Transitivity of Divisibility
• For all integers a, b and c, if a divides b and b divides c, then
a divides c.
Unique Factorization Theorem for Integers
• Given any integer n>1, there exist a positive integer k, distinct
prime numbers 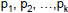 , and positive integers , and positive integers
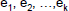
such that n can be uniquely represented in the standard
factored form: 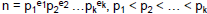 . .
(Proof in Section 10.4.) |
Quotient and Remainder Theory
• Given any integer n and positive integer d, there exist unique
integers q and r, such that n = dq + r and 0 ≤ r < d. (Proof in Sec
4.4.)
Definitions
Given a nonnegative integer n and a positive integer d,
• n div d: the integer quotient when n is divided by d.
• n mod d: the integer remainder when n is divided by d.
Symbolically, (n div d=q and n mod d =r) ↔ n=dq+r.
Definition
• The parity of an integer refers to the property of an integer to be
even or odd. |
Definitions (Floor and Ceiling)
• For any real number x, the floor of x, written
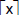 , is the unique , is the unique
integer n such that n ≤ x < n + 1. It is the max of all ints ≤ x.
(Symbolically,  ) )
• For any real number x, the ceiling of x, written
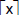 , is the , is the
unique integer n such that n – 1 < x ≤ n.
(Symbolically, 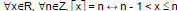 .) .)
Examples:
• If k is an integer, what are 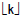 and and
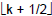 ? ?
• Is the statement 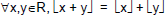 true? true? |
| Methods of Proof
Strategies
 Direct Proof Direct Proof
 Method of Exhaustion Method of Exhaustion
 Generalizing from the Generic
particular Generalizing from the Generic
particular
 Indirect Proof Indirect Proof
 Proof by Contradiction Proof by Contradiction
 Proof by Contraposition Proof by Contraposition
Cases
 Proving an
existential statement Proving an
existential statement
 Constructive vs non-constructive
proofs of existence Constructive vs non-constructive
proofs of existence
 Disproving an
existential statement (strategies above) Disproving an
existential statement (strategies above)
 Proving a
universal statement (strategies above) Proving a
universal statement (strategies above)
 Disproving a
universal statement Disproving a
universal statement
 Counterexample Counterexample |
Examples •
Show that there is a prime number that can be written as the
sum of two perfect squares.
• Disprove the following statement:
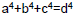 has no non-trivial whole number
solutions . has no non-trivial whole number
solutions .
(See a counterexample on P.139.)
• Prove or Disprove the following statements:
 For any
integers a, b, c: (a | b) → (a | bc). For any
integers a, b, c: (a | b) → (a | bc).
 For any
integers a, b, c: For any
integers a, b, c: 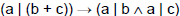 . .
|
| Methods of Proof
Direct Proof:
 Express the
statement in the form: Express the
statement in the form:
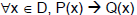
 Take a
particular but arbitrarily chosen x from D so that Take a
particular but arbitrarily chosen x from D so that
P(x) is true.
 Show that the
conclusion Q(x) is true based on definitions, Show that the
conclusion Q(x) is true based on definitions,
previous results , theorems and the rules for logical
inference. |
Examples Prove
the following:
• The sum of any two rational numbers is
rational.
• For all integers a, b and c, if a divides b and b
divides c, then a divides c.
• Any integer n>1 is divisible by a prime
number. |
| Examples Prove
the following:
(proof by cases)
• Any two consecutive integers have opposite
parity.
• The square of any odd integer has the form
8m+1 for some integer m.
|
Examples Prove
the following:
• For all real numbers x and all integers m,
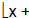
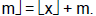
• For any integer 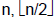 is n/2 for even n and (n– is n/2 for even n and (n–
1)/2 for odd n.
• For any nonnegative integer n and any positive
integer d, if 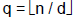 and and
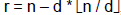 , ,
then n = d*q + r and 0 ≤ r < d. |
| Methods of Proof
Proof by Contraposition:
 Express the
statement in the form: Express the
statement in the form:
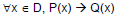
 Rewrite the
statement in the contrapositive form: Rewrite the
statement in the contrapositive form:
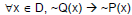
 Prove the
contrapositive by a direct proof: Prove the
contrapositive by a direct proof:
 Take a
particular but arbitrarily chosen x from D so that Take a
particular but arbitrarily chosen x from D so that
Q(x) is false.
 Show that the
conclusion P(x) is false. Show that the
conclusion P(x) is false. |
Examples Prove
the following:
• 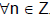 , n is even ↔ n2 is even. , n is even ↔ n2 is even.
|
| Methods of Proof
Proof by Contradiction:
 Suppose that the negation of the statement is true. Suppose that the negation of the statement is true.
 Show that this supposition leads logically to a Show that this supposition leads logically to a
contradiction .
 Conclude that the statement to be proved is true. Conclude that the statement to be proved is true.
|
Examples
Prove the following:•
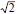 is irrational. is irrational.
• There is no integer that is both even and odd.
• The sum of any rational number and any irrational number is
irrational.
• For any integer a and any prime number p,
if p | a, then p does not divide (a + 1).
• The set of prime numbers is infinite. |
| Common Mistakes
Common mistakes in a proof
• Arguing from example
• Using the same symbol for different variables
• Jumping to a conclusion
• Begging the question
• Misuse of the word if |
|
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
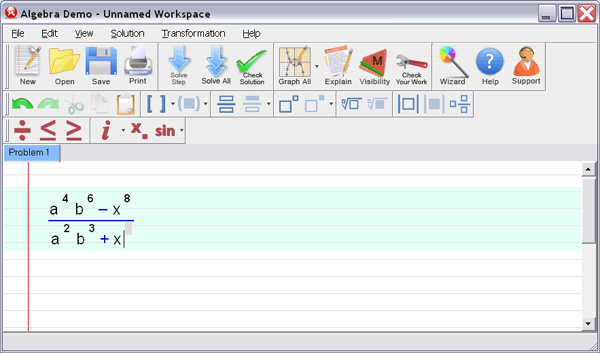
Step 2 :
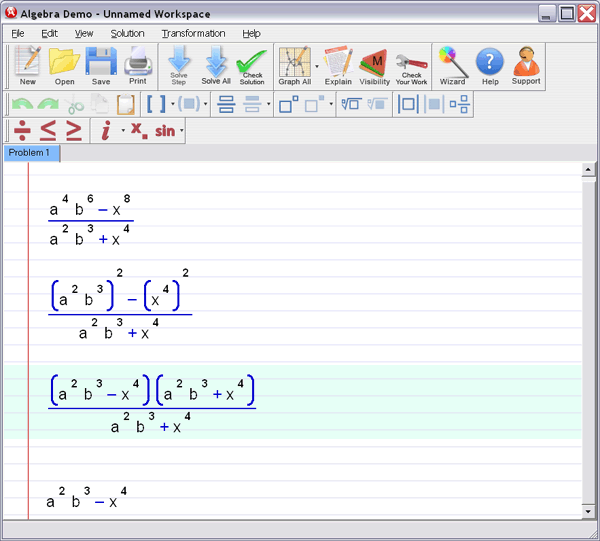
Let Algebra Helper solve it:
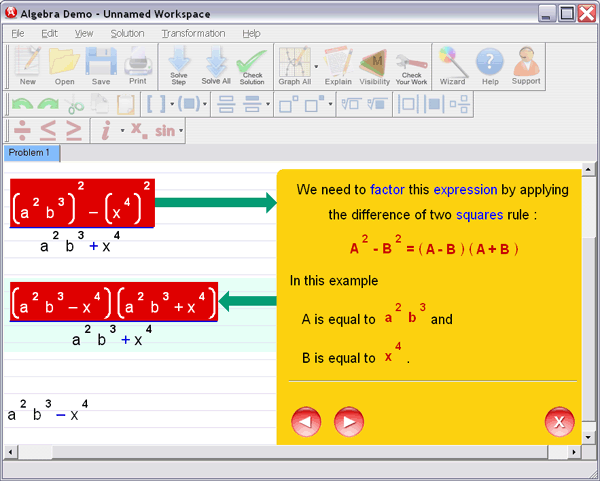
Step 3 : Ask for an explanation for the steps you don't understand:
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



