Outline
Today's lesson will cover some basic concepts of arithmetic.
Toward the end of the lesson, we will solve a few problems using
these concepts. The chapters that will be covered day are:

 1.3 and
1.5-Elementary Arithmetic
1.3 and
1.5-Elementary Arithmetic

 1.8, 1.9,
and 1.10-Applications
1.8, 1.9,
and 1.10-Applications
 1.3 Arithmetic
1.3 Arithmetic
The commutative law says that when you add or multiply
numbers, the order you add or multiply them does not matter. In
other words,
a + b = b + a.
The distributive law says that when a number is multiplied by the
sum of two numbers that it equals, that number multiplied by the
two numbers individually, with the results added afterward, that is,
(a + b) · c = a ·c + b · c.
 1.3 Order of Operations
1.3 Order of Operations
When a number is both preceded and followed by two binary
operations that are not the same, a rule is required for which
operation should be applied first, this rule is known as the order of
operations. So binary operations within parentheses outrank
exponents, exponents outrank multiplication and division (but
multiplication and division have equal rank), and these two
outrank addition and subtraction (which have equal rank).
 1.5 Adding and Subtracting Fractions
1.5 Adding and Subtracting Fractions
When adding fractions with the same denominator, the result is
the same as the sum of the numerators over the denominator. A
similar statement can be made for subtraction. If the fractions
have different denominators,
 First, find the least common denominator .
First, find the least common denominator .
 Then write equivalent fractions using this denominator.
Then write equivalent fractions using this denominator.
 Add or subtract the fractions.
Add or subtract the fractions.
 1.5 Adding and Subtracting Mixed Numbers
1.5 Adding and Subtracting Mixed Numbers
To add or subtract mixed numbers, simply convert the mixed
numbers into improper fractions, then add or subtract them as
fractions.
Example :
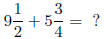
 1. 5 Multiplying Fractions and Fractions
1. 5 Multiplying Fractions and Fractions
When two fractions are multiplied, the result is a fraction with a
numerator that is the product of the fractions' numerators and a
denominator that is the product of the fractions' denominators.
Example :
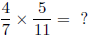
 1.5 Multiplying Mixed Numbers
1.5 Multiplying Mixed Numbers
To multiply mixed numbers, convert them to improper fractions
and multiply.
Example:
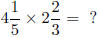
 1.5 Reciprocal
1.5 Reciprocal
The reciprocal of a fraction is obtained by switching its numerator
and denominator. To find the reciprocal of a mixed number, first
convert the mixed number to an improper fraction, then switch the
numerator and denominator of the improper fraction. Notice that
when you multiply a fraction and its reciprocal, the product is
always 1.
Example:
Find the reciprocal of 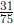 . We switch the
numerator and
. We switch the
numerator and
denominator to find the reciprocal: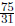 .
.
 1.5 Dividing Fractions
1.5 Dividing Fractions
To divide a number by a fraction, multiply the number by the
reciprocal of the fraction.
Example:
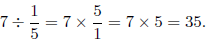
 1.5 Dividing Mixed Numbers
1.5 Dividing Mixed Numbers
To divide mixed numbers, you should always convert to improper
fractions, then multiply the first number by the reciprocal of the
second.
Example:
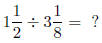
 1.8 Percentage
1.8 Percentage
To convert a fraction to a percentage, divide the numerator by the
denominator. Then move the decimal point two places to the right
(which is the same as multiplying by 100) and add a percent sign.
Example: Given the fraction 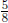 what is the
percentage?
what is the
percentage?
To change a percentage to a fraction, divide it by 100 and reduce
the fraction or move the decimal point to the right until you have
only integers.
 1.9 Proportions
1.9 Proportions
A proportion is a name we give to a statement that two ratios are
equal. It can be written in two ways:
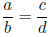
or
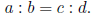
 1.13 Calculations: converting from one unit to another
1.13 Calculations: converting from one unit to another
The simplest way to carry out calculations involving different units
is to use the dimensional method . In this method, a quantity
described in one unit is converted to another by means of a
conversion factor. A conversion factor is ratio of two quantities
that have different units:
start quantity × conversion factor = equivalent quantity:
 1.15 Integers
1.15 Integers
The set containing the natural numbers, zero, and all negative
numbers is called the integers. The symbol Z is used to denote set
of integers. Some important properties of the integers:
 The sum or product of two integers is always an integer.
The sum or product of two integers is always an integer.
 The integers is an ordered set.
The integers is an ordered set.
 1.5 Addition and Subtraction of Integers
1.5 Addition and Subtraction of Integers
 Subtracting of an integer is equivalent to adding the opposite
Subtracting of an integer is equivalent to adding the opposite
or inverse of that integer.
 The absolute value of an integer represents the distance of
The absolute value of an integer represents the distance of
that integer from zero.
 When adding two integers of the same, add the absolute value
When adding two integers of the same, add the absolute value
of the integers. The sign of the sum is the same as sign of
both integers.
 When adding two integers of opposite signs, determine their
When adding two integers of opposite signs, determine their
absolute value and then subtract the smaller number from
larger number. The sign of the difference is the sign of larger
number
 1.16 Multiplication and Division of Integers
1.16 Multiplication and Division of Integers
 The product or quotient of two integers of the same sign is
The product or quotient of two integers of the same sign is
always positive .
 The product or quotient to two integers of opposite sign is
The product or quotient to two integers of opposite sign is
always negative.
 The quotient of two integers is not always an integer.
The quotient of two integers is not always an integer.
 1.16 Multiplication and Division of Integers
1.16 Multiplication and Division of Integers
 The product or quotient of two integers of the same sign is
The product or quotient of two integers of the same sign is
always positive.
 The product or quotient to two integers of opposite sign is
The product or quotient to two integers of opposite sign is
always negative.
 The quotient of two integers is not always an integer.
The quotient of two integers is not always an integer.
 4.1 Inequality symbols
4.1 Inequality symbols
 ≠ means not equal to
≠ means not equal to
 < means is less than
< means is less than
 > means is greater than
> means is greater than
 ≤
means less than or equal to
≤
means less than or equal to
 ≥
means greater than or equal to
≥
means greater than or equal to
 4.2 Solving inequalities
4.2 Solving inequalities
For real numbers a, b, and c.
 If a < b, then a + c < b + c.
If a < b, then a + c < b + c.
 If a < b, then a + c < b - c.
If a < b, then a + c < b - c.
Similar statements can be made for the symbols >, ≤, and ≥.
For real numbers a, b, and c.
 If a < b and c > 0, then ac < bc.
If a < b and c > 0, then ac < bc.
 If a < b and c < 0, then ac > bc.
If a < b and c < 0, then ac > bc.
 If a < b and c > 0, then a/c < b/c.
If a < b and c > 0, then a/c < b/c.
 If a < b and c < 0, then a/c > b/c.
If a < b and c < 0, then a/c > b/c.
Similar statements can be made for the symbols >, ≤, and ≥.
 4.3 Exponents and Polynomials
4.3 Exponents and Polynomials
 If n is a natural number, then
If n is a natural number, then 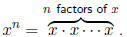
 If n and m are natural numbers, then
If n and m are natural numbers, then 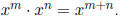
 If n and m are natural numbers, then
If n and m are natural numbers, then 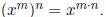
 If n is a natural number, then
If n is a natural number, then 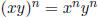 and if y ≠
0,
and if y ≠
0,
then 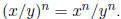
 4.4 The FOIL method
4.4 The FOIL method
FOIL is an acronym for First terms, Outer terms, Inner terms, and
Last terms. To use the FOIL method to multiply 2x - 4 by 3x + 5,
we
 Multiply the First terms 2x and 3x to get 6x2,
Multiply the First terms 2x and 3x to get 6x2,
 Multiply the Outer terms 2x and 5 to get 10x,
Multiply the Outer terms 2x and 5 to get 10x,
 Multiply the Inner terms -4 and 3x to get -12x, and
Multiply the Inner terms -4 and 3x to get -12x, and
 Multiply the Last terms -4 and +5 to get -20.
Multiply the Last terms -4 and +5 to get -20.
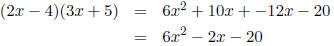
 4.5 Factoring Trinomials of the form x2 + bx + c
4.5 Factoring Trinomials of the form x2 + bx + c
 Find two integers whose product is constant term in the
Find two integers whose product is constant term in the
trinomial.
 There sum must equal the coefficient of the middle term.
There sum must equal the coefficient of the middle term.
 4.6 Factoring Trinomials of the form ax2 + bx + c
4.6 Factoring Trinomials of the form ax2 + bx + c
 Find the factors of the leading coefficient.
Find the factors of the leading coefficient.
 Find the factors of the last term.
Find the factors of the last term.
 Try combination of the first terms and last terms until you
Try combination of the first terms and last terms until you
find one that works.
 3.4 Linear functions
3.4 Linear functions
The slope of a line function is defined by
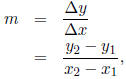
Where 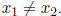
 3.4 Geometric Meaning of Slope
3.4 Geometric Meaning of Slope
From its geometric meaning, slope may be determined from a
graph by the formula

 3.5 Horizontal and Vertical Intercepts
3.5 Horizontal and Vertical Intercepts
Definition: A horizontal intercept of a graph is a point where the
graph crosses the horizontal axis. The ordered pair notation for a
horizontal intercept has the form (a, 0), where a is the input value.
Definition: A vertical intercept of a graph is a point where the
graph crosses the vertical axis. The ordered pair notation for a
vertical intercept has the form (0, b), where b is the output value.



