Equations and Inequalities with Absolute Value

Chapter 5, Section 2: Adding and Subtracting Polynomials

Def1. Like (similar) terms are terms that have the same variables with the
same exponents .

EX1. Write 3 other terms that are like (similar) to 2x²y

EX2. Write 3 other terms that are not like (similar) to 2x²y

Note1. To add ( subtract ) like terms, add (subtract) their numerical
coefficients and affix their common variable part.

EX3. Add 3xyz and -8xyz

EX4. Subtract 5rs³ from 2rs³

EX5. Simplify by combining like terms:5pqr + pqr - 2pqr

EX6. Simplify by combining like terms:
3a²b - 2ab² + a²b - 5ab² + a²b²

Note2. The distributive property of multiplication over addition:
a(b + c) = ab + ac

EX7. Simplify: (-2x² + 6x + 5) - (-4x² - 7x + 2)

EX8. Simplify: 3(y² + 2y) - 4(y² - 4) + 2(y - 3)

EX9. Write a polynomial that represents the perimeter of the quadrilateral
shown below:

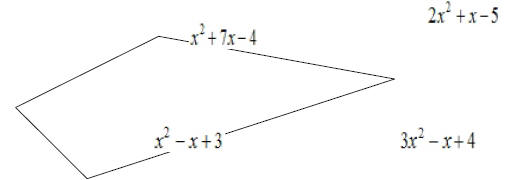
EX10. Draw and label a scalene triangle whose perimeter is
5y² - 4y + 6

EX10. Draw an label an isosceles triangle whose perimeter is
5y² - 4y + 6

EX11. Suppose that you bought a house in 2006 for $150,000. Because of
the national housing market disaster, this house is depreciating at the
rate of $8000 per year. (A) Write a polynomial function that will
give you the value of this house in x years. (B) Find the value of the
house in 2010.

Chapter 5, Section 3: Multiplying Polynomials

Recall:
x^ax^b = x^a+b
(x^a)^b = x^ab

Note1: To multiply one monomial by another, multiply the numerical factors
and multiply the variable factors .

EX1. (3x²yz³)(4xy⁴z⁵)

EX2. (-2ab²c)(-3abc⁴)(-a²b)

Note2. To multiply a polynomials by a monomial, use the distributive
property and multiply each term of the polynomial by the monomial.

EX3. 3a(4a² + 3a - 4)

EX4. -4r²s(2r²s² - 3rs² + 5rs)

Note 3. To multiply a polynomial by a polynomial, use the distributive
property repeatedly.

Special Case. To multiply a binomial by a binomial , use the distributive
property twice. This process is often referred to as F.O.I.L.

The meaning of F.O.I.L. in this process of multiplying two binomials is

F=the product of the first terms
O=the product of the outer terms
I= the product of the inner terms
L=the product of the last terms

EX5. (3t - 2)(4t + 3)

EX6. (2a - b)(2a +b)

EX7. (x³ + 3y²)(x²+2y)

EX8. (y + 4)²

EX9. (a + b)²

Note3. The square of a binomial is a __________________________.

EX10. (2A - B)(4A² + 3AB - B²)

EX11.

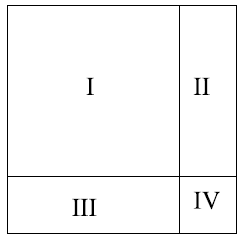
A) What is the length of each side of the largest square shown in
the figure above?

B) Find the area of the largest square by using its side length.

C) Find the area of each part of the largest square.

D) Add the areas that you found in part (C).

E) Compare your answers to parts (B) and (D). What should be
true and why?

Chapter 5, Section 4: The Greatest Common Factor and Factoring by
Grouping

Def. Prime number–a natural number that has exactly two distinct factors
Question: What does it mean to say that “x is a factor of y”?

EX1. Find all the factors of 24.
Find all the factors of 90.
Find the common factors of 24 and 90.
What is the Greatest Common Factor , GCF, of 24 and 90?
What does it mean to say that “x is the GCF of y”?

EX2. Using prime factorization to find the GCF.
Find the prime factorization of 24 and 90.

Note1. The GCF of the two numbers will be a product the prime number
factors common to the two numbers with each common prime
number factor raised to the lowest power on that factor in either
factorization.

EX3. Use the method of prime factorization to find the GCF (280 and 294).

EX4. Find the GCF of a²b³c and a⁴bd

EX5. Find the GCF of 18x²y and 24xy³

Note2. To factor a polynomial, find the GCF of each term of the
polynomial and use the distributive property: ab + ac = a(b + c)

EX6. Factor 18x²y + 24xy³

EX7. Factor 30r²s²t - 40r³st⁴

EX8. Factor 14r²s³ + 15t⁴

EX9. Factor 9m⁴n³p² + 36m²n³p⁴ - 18m²n³p⁵

EX10. Factor 25t⁴ - 10t³ + 5t²

EX11. Factor -18a²b + 12ab³

EX12. Factor 5(a - b) - c(a - b)

Method 2: Factoring by Grouping

EX13. Factor ac + ad + bc + bd

EX14. Factor 2c + 2d - cd - d²

EX15. Factor x² - ax - xy + ay

Literal Equations : In this type of problem, you will be given an equation and
asked to solve for one of the variables in terms of the other
variables.

EX16. Solve r₁r₂ = rr₁ + rr₂ for r.

EX17. Solve H(a + b) = 2ab for a.

EX18. Solve x(5y + 3) = y for y.

EX19. Solve AL + GE = BRA for A.